Markus Kahn
- 110
- 14
- Homework Statement
- The ultimate goal is to find the equations of motion for a piece of toast falling from a table.
- Relevant Equations
- Euler-Lagrange equations.
First of all, disclaimer: This isn't an official assignment or anything, so I'm not even sure if there is a resonably simple solution.
Consider the following sketch.
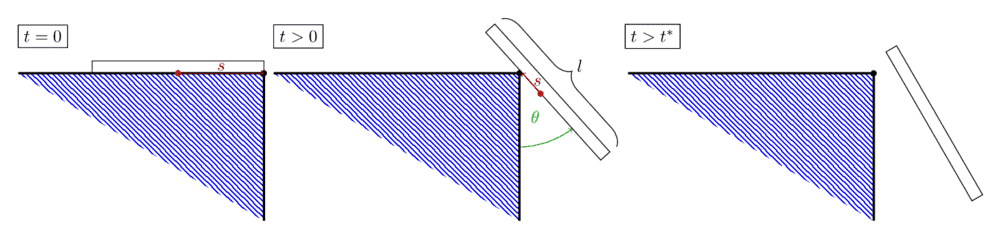
(Forgive me if it isn't completely clear, I didn't want to fiddle around for too long with tikz...)
Let us assume that we can approximate a piece of toast as a rectangle with homogenous mass distribution ##m## and length ##l##. We further assume that for ##t=0## the toast has velocity in positive ##x## direction. We can describe the system over the two generalized coordinates ##s## and ##\theta##, where ##s## gives the distance from the center of mass to the coordinate frame center (let us for now assume that the toast is infinitely thin... Not sure if this is necessary though) and ##\theta## beeing the angle between the toast and the ##y## axis. We can then write for the center of mass
$$\vec{x}_p = s(t)\begin{pmatrix}\sin(\theta(t))\\-\cos(\theta(t))\end{pmatrix}.$$
We find therefore for the kinetic and potential energy
$$T=\frac{1}{2}m\dot{x}_p^2 = \frac{1}{2}m (\dot s ^2 + s^2\dot \theta^2)\quad\text{and}\quad V=-mg s\cos(\theta),$$
which therefore would result in the following Lagrange function
$$L = \frac{1}{2} m (2 g \cos(\theta(t)) s(t) + \dot s(t)^2 +
s(t)^2 \dot \theta (t)^2).$$
Is this correct up until here? Finding the eom's isn't really a problem if this is correct..
PS: the third picture should just indicate that one can find ##t^*## with the condition ##(\ddot{x_p})_x\overset{!}{=}0## for which the toast loose its contact to the table.
Consider the following sketch.
(Forgive me if it isn't completely clear, I didn't want to fiddle around for too long with tikz...)
Let us assume that we can approximate a piece of toast as a rectangle with homogenous mass distribution ##m## and length ##l##. We further assume that for ##t=0## the toast has velocity in positive ##x## direction. We can describe the system over the two generalized coordinates ##s## and ##\theta##, where ##s## gives the distance from the center of mass to the coordinate frame center (let us for now assume that the toast is infinitely thin... Not sure if this is necessary though) and ##\theta## beeing the angle between the toast and the ##y## axis. We can then write for the center of mass
$$\vec{x}_p = s(t)\begin{pmatrix}\sin(\theta(t))\\-\cos(\theta(t))\end{pmatrix}.$$
We find therefore for the kinetic and potential energy
$$T=\frac{1}{2}m\dot{x}_p^2 = \frac{1}{2}m (\dot s ^2 + s^2\dot \theta^2)\quad\text{and}\quad V=-mg s\cos(\theta),$$
which therefore would result in the following Lagrange function
$$L = \frac{1}{2} m (2 g \cos(\theta(t)) s(t) + \dot s(t)^2 +
s(t)^2 \dot \theta (t)^2).$$
Is this correct up until here? Finding the eom's isn't really a problem if this is correct..
PS: the third picture should just indicate that one can find ##t^*## with the condition ##(\ddot{x_p})_x\overset{!}{=}0## for which the toast loose its contact to the table.
Last edited by a moderator: