The response of a mass suspended between two poles to an angle of heel

[stavsantis]

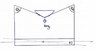
I am currently conducting a project where a yacht will be suspended in air by two straps which are connected together by two poles. The poles will be mounted on a barge and therefore I want to find how I can relate the angle of heel ($\varphi$) to the two angles. Although the yacht will remain upright and not heel with the motion of the barge, due to its keel, it is free to slide along the strap to the most natural position. I attached a simplified 2D sketch of what I mean. In the level condition θl = θr. Any insight or where I can look to find the solution to my problem would be greatly appreciated!

 

[OldEngr63]

Draw the picture in the heeled condition, and then you should be in a position to start writing the governing equations.

 

[stavsantis]

But how will I know the exact position of the mass when the structure is heeled? would it just be by deriving the forces in the x and y directions??

 

[OldEngr63]

You can treat it as a dynamics problem,and thus try to solve for the dynamic position of the mass, or you can treat it as a statics problem and solve for the static position of the mass. Either way, you start with summing forces on the mass in an unknown position.