Thermo - Heat Engines, Heat Pumps

[brendan714]

So I wrote my Thermodynamics final today and one of the questions were as follows:

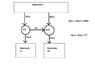
A reversible heat engine supplies a reversible heat pump. Both draw off of a temperature reservoir T (can't remember the exact value, but there was one). The heat engine discharges heat into TL, and the heat pump discharges heat into TH.

You know that QH for the Heat Engine (heat drawing from reservoir T) and QL for the Heat Pump (heat drawing from reservoir T) together equal 5 MW.

What is the total amount of heat discharged by the Heat Engine and the Heat Pump into their respective reservoirs?


I just simply said that the answer must be 5 MW since both are reversible (no losses anywhere)! Does anyone agree/think I am wrong?
Thanks!

 

[Andy Resnick]

You did not account for the work the heat engine did on the heat pump (if I'm imagining the system correctly), but I can't say more than that right now.

 

[brendan714]

Please find attached my drawing of the system, which was given on the exam.

What if you assume that all of the work generated by the heat engine is used to power the heat pump?

But then comes the question, is that a valid assumption?

Thanks for the response.

 

[Andy Resnick]

Are you sure there's no typo in the drawing?

 

[russ_watters]

I would think 5 mw is a possibility, but it would depend on the CoP/eff of each. I don't think there's actually enough information provided.

 

[brendan714]

I do confirm that the diagram is correct.

Keep in mind that they DID specify the values of T, TL and TH, I just can't remember them.
Also remember that both the heat pump and the heat engine are reversible.

I talked to some other people and they got 5 as well so that makes me feel a little bit better. The only problem is the majority of the people I talked to got something way bigger than 5...
I'm just intrigued by this question because it seems so easy!

Thanks for the responses!

 

[Andy Resnick]

If the diagram is correct, then the heat pump has an efficiency of zero.

 

[brendan714]

Why do you say that?

I thought that since they were reversible the efficiencies were as follows:

\eta HE = W / QH1 = 1 - (TL/T)

and COP HP = QH2 / W = 1 / (1 - (T/TH))

unless I am misstaken.

 

[Andrew Mason]

For the heat engine:

\eta = \frac{W}{Q_{he}} = 1 - \frac{T_c}{T_h}

Q_{he} = \frac{W}{1 - \frac{T_c}{T_h}}

For the heat pump:

COP = \frac{Q_{hp}}{W} = \frac{1}{1-\frac{T_c}{T_h}}

Q_{hp} = \frac{W}{1 - \frac{T_c}{T_h}}Since the work done by the heat engine is equal to the work done by the heat pump,

Q_{he} = Q_{hp}

Since W = Q_h - Q_c, Q_c is the same for both (ie. Q_{ce} = Q_{cp}).

So if Q_{ce} + Q_{hp} = 5 mW then Q_{cp} + Q_{he} = 5 mW.

AM

 

[brendan714]

I think you are making a slight error with your assumptions above.

The shared reservoir, T, is Th for the heat engine and Tc for the heat pump (heat engine takes from a high temp reservoir and dumps into low).

Q,HE = W / (1 - (TL / T) )
Q,HP = W / (1 - (T / TH) )

They certainly aren't equivalent are they? Each reservoir is a different temperature.

 

[Andy Resnick]

Why do you say that?

I thought that since they were reversible the efficiencies were as follows:

\eta HE = W / QH1 = 1 - (TL/T)

and COP HP = QH2 / W = 1 / (1 - (T/TH))

unless I am misstaken.

I did it in terms of the heat flow: the efficiency of a Carnot process is Work/(heat absorbed) = 1-(heat emitted)/(heat absorbed)= 1-(refrigerator temp)/(furnace temp)

W/Q_H1 = 1-Q_L/Q_H1 for the engine
-W/Q_H2 = 1- Q_H2/Q_H2 for the pump.

So the efficiency of the pump is zero-work goes in, but the heat out is the same as the heat in. This contradicts the efficiency written in terms of temperatures, which is why I asked about the typo.

Using temperatures, I get Q_H1+Q_H2 = Q_H2(T/T+)+Q_H1(T-/T), where the engine couples to T- (<T) and the pump couples to T+ (>T). If T+ and T- != T, I'm not sure that expression can be reconciled.