- #1
NickDime
- 6
- 0
- Homework Statement
- What mass of steam initially at 130°C is needed to warm 200 g of water in a 100-g glass container from 27.0°C to 42.0°C? If we instead used 78.0 g of water, how much 100°C steam remains in thermal equilibrium?
- Relevant Equations
- Q = mc(delta)T, Q = L(delta)m, Q(cold) = -Q(hot)
c(water)= 4186 J/kg*C, c(steam)= 2010, c(glass)= 837. L(water, vaporizing)= 2.26e6 J/kg
The second question is where I'm lost. The answer to the first question is 5.39 grams. The second is 10.3 grams. Until I saw the answer I was setting the equation up as if some of the original steam had condensed. But it appears that some of the original water changed into steam. Is it necessary to know before hand whether its the water or steam that undergoes the phase change? My attempt at a solution was to set Q(cold)=-Q(hot).
subscripts... w = water, s = steam, g = glass, v = vaporization
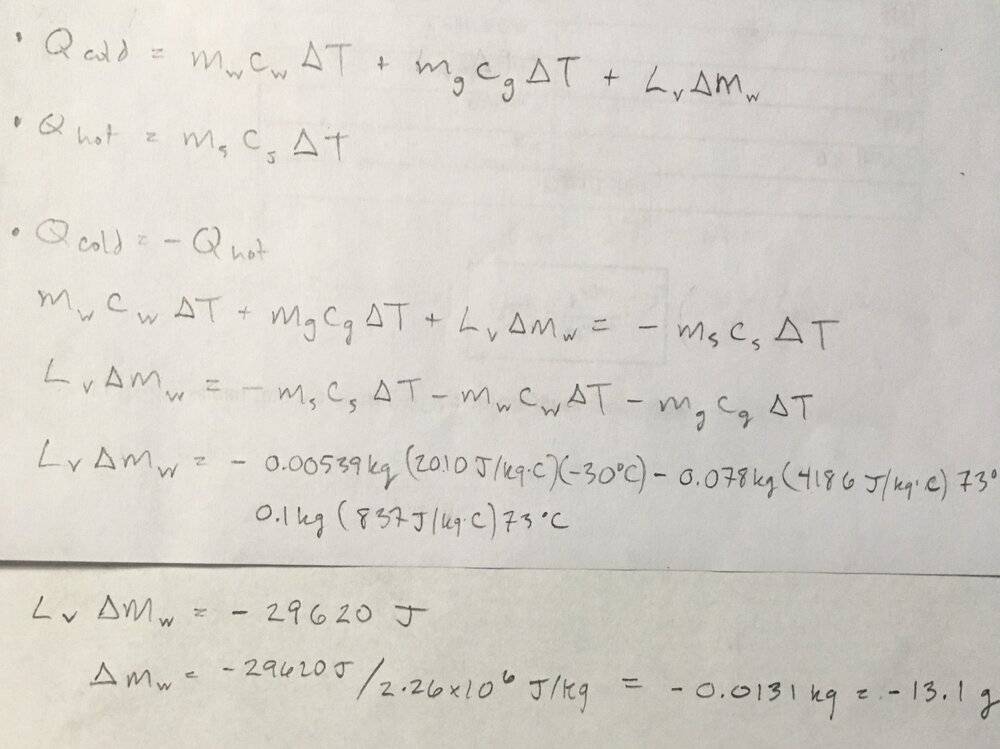
subscripts... w = water, s = steam, g = glass, v = vaporization