solidbastard
- 6
- 0
MODERATOR NOTE - NO TEMPLATE BACAUSE POSTED IN GENERAL PHYSICS
I am having trouble attacking this problem properly and getting the right solution, which I do not have. (only know I did it wrong on exam).
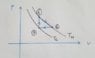
Anyway, there is picture attached this is a cycle of some working material that has a total energy of U= alpha*T^4
I need to determine:
To solve it is going to use this or?
So not sure if in total calculation should take in mind changes in p, T and V or what? Becuase T is changing always?
Anyway, thanks for help if anyone has solution :
I am having trouble attacking this problem properly and getting the right solution, which I do not have. (only know I did it wrong on exam).
Anyway, there is picture attached this is a cycle of some working material that has a total energy of U= alpha*T^4
I need to determine:
- Change of total energy from 1 to 2.
- Heat that came from 3 to 1.
To solve it is going to use this or?
Code:
$(\frac{\partial U}{\partial V})\cdot dV + (\frac{\partial U}{\partial T})\cdot dT + (\frac{\partial U}{\partial p})\cdot dp$Anyway, thanks for help if anyone has solution :
Attachments
Last edited by a moderator: