MathError
- 23
- 0
- Homework Statement
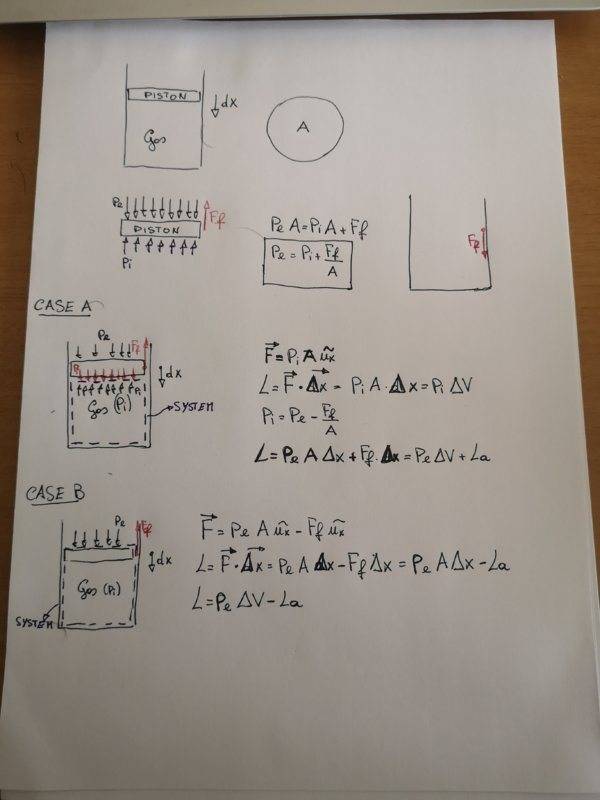
- Find the expression of work during the compression of a gas in presence of friction froce between piston and cylinder
- Relevant Equations
- P_e=external pression;
P_i=pression of the gas inside the cylinder (uniform pression);
F_f=friction force;
L=work on the system
L_a=friction work
Q=exchanged heat
E_t=total energy;
mass of piston=0;
A=area of the piston
Hi guys,
First of all I'm sorry for my bad english I'll try to be as clear as possible.
I have tried to solve this problem to understand the First Law of Thermodinamics: Q+L=ΔE_t
In fact I know L (in the current convention) is the work which the envirorment does on the system but I don't understand which contributes I have to include in L.
let we start from simple case: in this case F_f=0, so there is no friction force between piston and cylinder. In the hypothesis of quasistatic process the resulting force on the piston is zero so:
P_e=P_i.
The work made by envirornment on the system can be calculated as:
L=P_e*A*Δx=P_e*ΔV=P_i*ΔV
If there is friction force the problem becomes more complicated.
First all since the resulting force on the piston is still zero, in the hypothesis of compression we can find that:
P_e=P_i+F_f/A;
Also, there are two friction forces: the first one which is applied on the piston and it's considered in the previous equation and a second one which is applied on the cylinder but which doesn't produce work because it's applied to fixed points.
Now we have to choose our system: we can consider only the gas (A) or system which includes gas and piston (B).
Case A
In this case, in my opinion, the force on the system is:
F=P_i*A
In fact external pressure and friction force aren't applied to the surface of control of the system but to the piston.
As you can see in the photo, the the resulting work is:
L=P_e*ΔV+L_a
Case B
Including the piston in the system, the external forces applied to the surface of control are:
F=P_e*A-F_f
In this case the resulting work is different from the previous one and it values:
L=P_e*ΔV-L_a
I think both the results are wrong, anyway it's impossibile the two works are different because I only changed the point of view of the system. I hope I have been enough clear and
 you can give me an help.
you can give me an help.
Thanks you
First of all I'm sorry for my bad english I'll try to be as clear as possible.
I have tried to solve this problem to understand the First Law of Thermodinamics: Q+L=ΔE_t
In fact I know L (in the current convention) is the work which the envirorment does on the system but I don't understand which contributes I have to include in L.
let we start from simple case: in this case F_f=0, so there is no friction force between piston and cylinder. In the hypothesis of quasistatic process the resulting force on the piston is zero so:
P_e=P_i.
The work made by envirornment on the system can be calculated as:
L=P_e*A*Δx=P_e*ΔV=P_i*ΔV
If there is friction force the problem becomes more complicated.
First all since the resulting force on the piston is still zero, in the hypothesis of compression we can find that:
P_e=P_i+F_f/A;
Also, there are two friction forces: the first one which is applied on the piston and it's considered in the previous equation and a second one which is applied on the cylinder but which doesn't produce work because it's applied to fixed points.
Now we have to choose our system: we can consider only the gas (A) or system which includes gas and piston (B).
Case A
In this case, in my opinion, the force on the system is:
F=P_i*A
In fact external pressure and friction force aren't applied to the surface of control of the system but to the piston.
As you can see in the photo, the the resulting work is:
L=P_e*ΔV+L_a
Case B
Including the piston in the system, the external forces applied to the surface of control are:
F=P_e*A-F_f
In this case the resulting work is different from the previous one and it values:
L=P_e*ΔV-L_a
I think both the results are wrong, anyway it's impossibile the two works are different because I only changed the point of view of the system. I hope I have been enough clear and
Thanks you
Last edited by a moderator:
