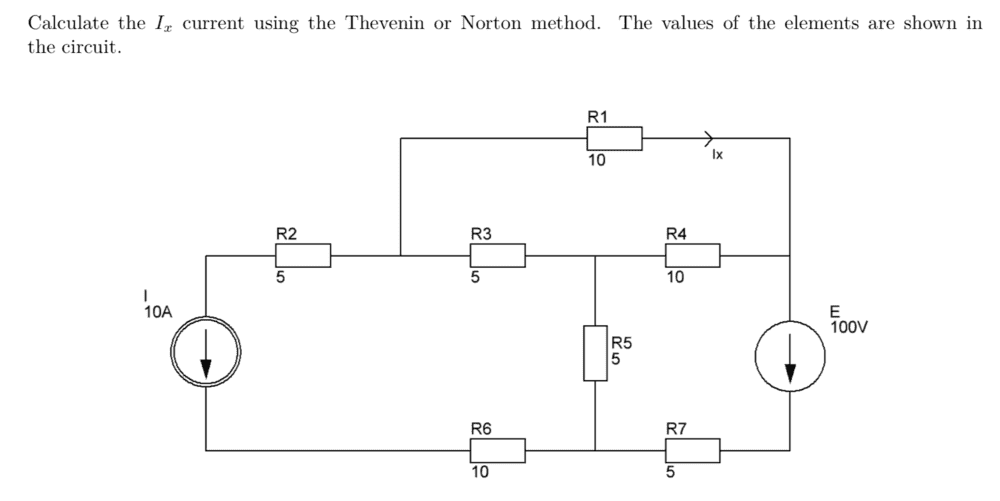
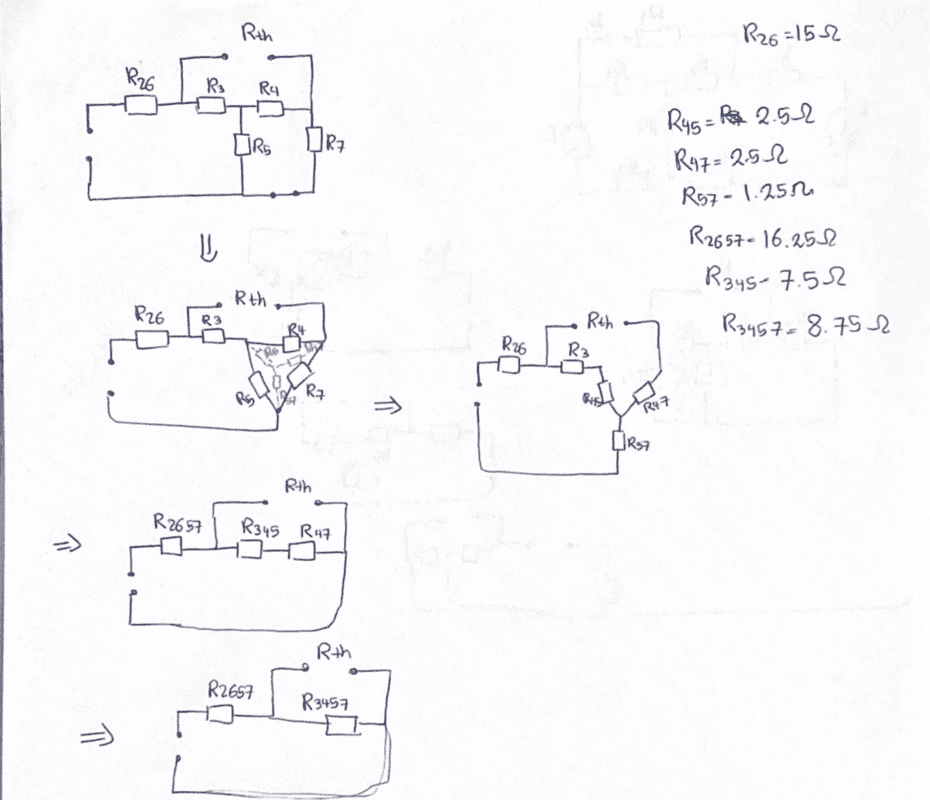
SUMMARY
The discussion centers on using Thevenin's Theorem to simplify circuits for calculating equivalent resistance (Rth). Participants debate the necessity of delta-star transformations for resistors R5 and R7, ultimately concluding that they are in series, thus negating the need for such transformations. The final method for determining Rth involves connecting a voltage source between terminals and measuring the current supplied. The conversation also touches on the implications of ideal current sources and their effect on circuit analysis.
PREREQUISITES
- Understanding of Thevenin's Theorem
- Familiarity with delta-star transformations
- Knowledge of series and parallel resistor configurations
- Basic circuit analysis techniques, including mesh analysis
NEXT STEPS
- Study Thevenin's Theorem applications in circuit simplification
- Learn about delta-star transformation techniques in detail
- Explore advanced circuit analysis methods, including mesh and nodal analysis
- Investigate the behavior of ideal current sources in circuit design
USEFUL FOR
Electrical engineering students, circuit designers, and anyone involved in circuit analysis and simplification techniques will benefit from this discussion.