RJVoss
- 11
- 0
This was a problem on an exam I had the other day and I want to know if my attempt was correct.
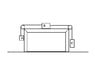
Please look at the attached image. You have a system of two ideal pulleys set up on a table. Block A is hanging from a string on the left side of the table which passes by a pulley connecting it to block B. Block B is resting on the table, and the kinetic coefficient of friction between the surface of the table and the block is 0.557. Block C is hanging from a string on the right side of the table which passes by a pulley and is attached to Block B. Block C is four times as massive as block A, and block B is three times as massive as block A. When the system is released from rest, block C accelerates downward until it reaches the floor, a distance of 105cm.
Find: The acceleration of block C and the time it takes to reach the ground.
F=ma
FF=\mukN
y = y0 + v0yt + 1/2 at2
N = mg
I started by trying to find the net force acting on block B in order to find the acceleration of the system. In this case,
Fnet= FC - (FA + FF)
so
Fnet= (4mAg) - 1mAg - (\mu3mAg)
simplify
Fnet= 3mAg(1-\mu)
because mB=3mA you can rephrase the above equation
Fnet= mBg(1-\mu)
so the acceleration of block B would be g(1-\mu), and plugging in the values I got the answer -4.34m/s2 rounded to three figures. This would also be the acceleration of block C.
Next I needed to find the time it took block C to hit the ground.
y = y0 + v0yt + 1/2 at2
so
y = 1/2 at2
t = sqrt(2y/a)
t = sqrt(2*-1.05m/-4.34m/s2)
t = 0.695s rounded to three figures
Did I do this problem correctly? And if not, can you please show me the correct way of doing a problem like this? Thanks.
Homework Statement
Please look at the attached image. You have a system of two ideal pulleys set up on a table. Block A is hanging from a string on the left side of the table which passes by a pulley connecting it to block B. Block B is resting on the table, and the kinetic coefficient of friction between the surface of the table and the block is 0.557. Block C is hanging from a string on the right side of the table which passes by a pulley and is attached to Block B. Block C is four times as massive as block A, and block B is three times as massive as block A. When the system is released from rest, block C accelerates downward until it reaches the floor, a distance of 105cm.
Find: The acceleration of block C and the time it takes to reach the ground.
Homework Equations
F=ma
FF=\mukN
y = y0 + v0yt + 1/2 at2
N = mg
The Attempt at a Solution
I started by trying to find the net force acting on block B in order to find the acceleration of the system. In this case,
Fnet= FC - (FA + FF)
so
Fnet= (4mAg) - 1mAg - (\mu3mAg)
simplify
Fnet= 3mAg(1-\mu)
because mB=3mA you can rephrase the above equation
Fnet= mBg(1-\mu)
so the acceleration of block B would be g(1-\mu), and plugging in the values I got the answer -4.34m/s2 rounded to three figures. This would also be the acceleration of block C.
Next I needed to find the time it took block C to hit the ground.
y = y0 + v0yt + 1/2 at2
so
y = 1/2 at2
t = sqrt(2y/a)
t = sqrt(2*-1.05m/-4.34m/s2)
t = 0.695s rounded to three figures
Did I do this problem correctly? And if not, can you please show me the correct way of doing a problem like this? Thanks.