Three Charges in an Electric Field

[blue_lilly]

Homework Statement

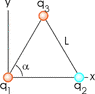
Three charges, q1 = 8.43nC, q2 = -4.29nC and q3 = 3.00nC are at the corners of an equilateral triangle, as shown in the figure below.

A. The angle alpha is 60.0° and L = 0.448 m. We are interested in the point midway between the charges q1 and q2 on the x axis.
For starters, calculate the magnitude of the electric field due only to charge q3 at this point.

B. Now calculate the magnitude of the electric field from all three charges at a point midway between the two charges on the x axis.

C. Calculate the angle of the electric field relative to the positive (to the right) x-axis, with positive values up (Counter-Clock Wise) and negative down (Clockwise). (enter the answer with units of deg)

D. If a tiny particle with a charge q= 1.41nC were placed at this point midway between q1 and q2, what is the magnitude of the force it would feel?

Homework Equations

W=Fdcosθ=(qE)dcosθ
lFl= (1/4 pie r^3)* (lq1l lq2l/r^2)

The Attempt at a Solution

A. (8.99E9)((3E-6)^2)=.08091
Then i found the distance from 3 to the midpoint. .224tan60=.387
.08091/.387=.209N/C
B. (8.99E9)((8.43E-6)(4.29E-6)(3E-6)/.224^2)=1.95E-5
C. An equilateral triangle is 180 degress and each angle is 60


I am so confused, any help would be greatly appreciated.

 

[Simon Bridge]

I am so confused, any help would be greatly appreciated.

That's OK - but we need to know where you are confused in order to help you.
Your attempts do not have units, nor do they show your method - things that would help us figure out where you are confused.

Do you know the equation for the electric field due to a single charge q at distance r?
Do you know the relation between electric field and electric force?

You appear to be able to do it for one charge.
The point you are interested in is (x,y)=(L/2,0)
Part A just needs the distance from q3 to the point.
Part B & C is the vector sum of the electric fields due to each charge. You already know how to add vectors.
Part D is a matter of turning $\vec{E}$ into $\vec{F}$.