To find direction and magnitude of forces acting in a system

[gnits]

Homework Statement

To find direction and magnitude of forces acting in a system

Relevant Equations

moments and force balancing

Please could I ask for help with the following:

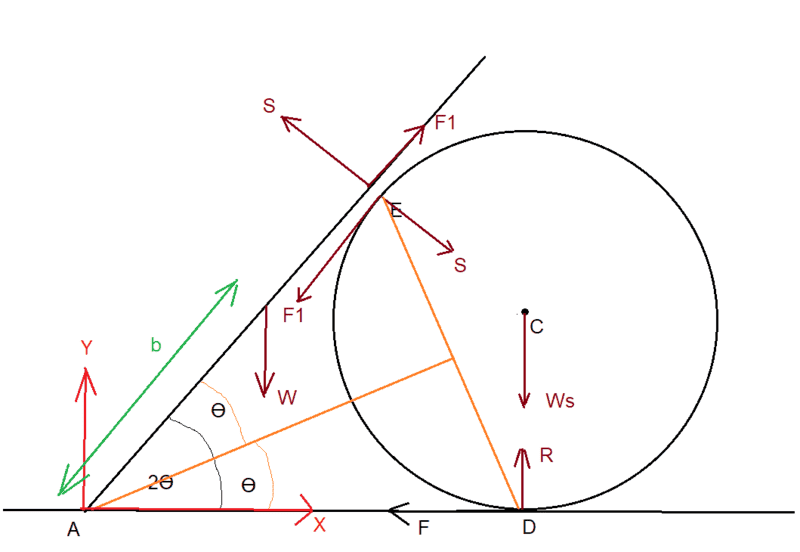
Here is my diagram, I show the rod displaced from the sphere so as to label the internal forces acting on each of the rod and the sphere:

In the diagram below I have added the line through DE at angle ꞷ the the horizontal, and a few other angles.

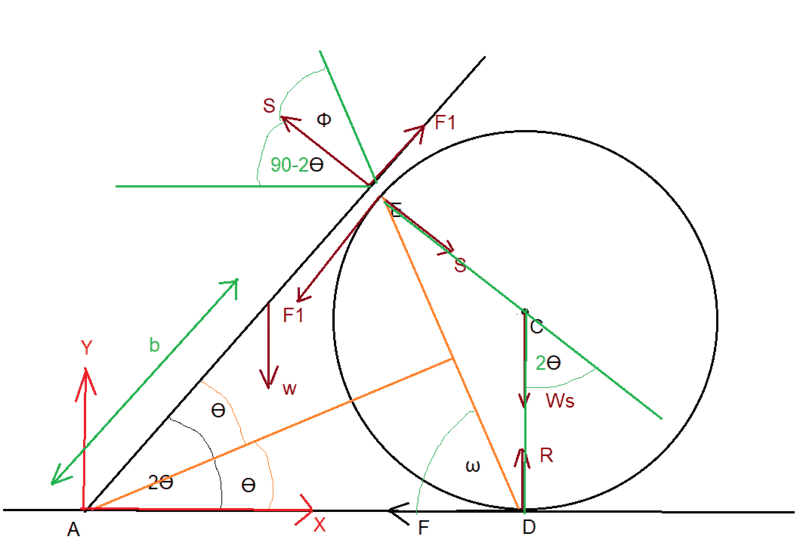
From sum of angles in triangle ADE = 180 I have:

ꞷ = 90 - ϴ

Here's my plan of attack:

I need to show that the angle which the resultant of S and F1 makes with he horizontal is ꞷ, the same as that of line connecting D and E. If I can do this then I will have answered the first part of the question.

So I need to show that 90 - 2ϴ + Φ = 90 - ϴ

i.e. that:

Φ = ϴ

Considering only the sphere and taking moments clockwise about D I have:

S * a * sin(2ϴ) - F1 * a * (1 + sin(90 - 2ϴ) ) = 0

which gives:

S = F1 * (1 + cos(2ϴ)) / sin(2ϴ)

So I know that S is (1 + cos(2ϴ)) / sin(2ϴ) times bigger that F1. So:

tan(Φ) = F1 / S = sin(2ϴ) / (1 + cos(2ϴ) )

Well, this isn't getting me nearer to showing that Φ = ϴ.

Thanks for any help...

 

[TSny]

tan(Φ) = F1 / S = sin(2ϴ) / (1 + cos(2ϴ) )

Well, this isn't getting me nearer to showing that Φ = ϴ.

Use trig identities for sin(2ϴ) and cos(2ϴ).

But there is an easier way to show that the net force $\vec F_E$ acting on the sphere at point E acts along ED. You have shown that you realize that $\vec F_E$ produces zero torque about D.

 

[gnits]

Use trig identities for sin(2ϴ) and cos(2ϴ).

But there is an easier way to show that the net force $\vec F_E$ acting on the sphere at point E acts along ED. You have shown that you realize that $\vec F_E$ produces zero torque about D.

Thanks very much. I was so close with my method but didn't know it. Will look for the simpler route you hint at also and then I'll move move on to the next part, that of having to actually find the magnitudes of S and F1.

Thanks again,
Mitch.