JwdePhysics
- 13
- 0
Homework Statement
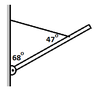
There is a lever rod of length 3.43 m, weight 44 N and uniform density. The lever rod is
pivoted on one end and is supported by a cable attached at a point 0.902 m from the other end. The lever rod is in equilibrium at angle of 68◦ from the vertical wall. The cable makes angle of 47◦ with the rod. I want to know the tension in the cable.
Homework Equations
Since everything at equilibrium all net forces and the net torque are equal to 0.
Fnetx=Horizontal Tension-Normal Horizontal Force=0
Fnety=Vertical Tension-Normal Vertical Force-The weight=0
tNet = Torque caused by the cable- Torque caused by the rod=0
The Attempt at a Solution
Well, in order to get the horizontal and vertical forces of the tension, I need the angle that makes the altitude of a triangle from the vertex connecting the tension cable and the rod. So if we draw the altitude we now have a right triangle.
-One of the vertices in the triangle is 65 degrees since it is also a vertex in the triangle created by the lever rod, the cable, and the wall. Therefore since a triangle has 180 degrees, we subtract 68 and 47 and then get 65 as the angle for that vertex
-The other angle must be 25 since there are 180 degrees in a triangle and 180-90-65=25.
So now we can update the equations like this:
Fnetx=Tcos(25)-Nh=0
Fnety=Tsin(25)-Nv-44=0
tNet=T((L-0.902)*sin(25))-44(L/2)=0
and therefore plugging in 3.43 for L will yield
T = 44(3.43/2)/((3.43-0.902)*sin(25))
And solving for T gives out 70.63.