DracoMalfoy
- 88
- 4
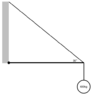
Homework Statement
n the diagram below, the horizontal bar has a length of 4m. The force due to the wire angled at 30 degrees is 1200N. What is the weight of the horizontal bar?
Homework Equations
T=F⊥r
The Attempt at a Solution
I know that I need to add the three( the bar, the wire, and weight, but I'm not sure how to do that. I tried...
0= Tbar+Twire+Tweight
0= -Tbar+-Twire+-Tweight
0= Tsin30+-1200sin30+-400sin30⋅9.8
I'm not sure if I did this correctly. The options for answers are
A) 6640N
B) 1600N
C) 3320N
D) 4200N
E) 2750N
The first answer that i got using another method was 3320. That was wrong.