- #1
maxverywell
- 197
- 2
According to the wikipedia article about the transition dipole moment:
When an atom or molecule interacts with an electromagnetic wave of frequency
 , it can undergo a transition from an initial to a final state of energy difference
, it can undergo a transition from an initial to a final state of energy difference
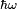 through the coupling of the electromagnetic field to the transition dipole moment.
through the coupling of the electromagnetic field to the transition dipole moment.
https://en.wikipedia.org/wiki/Transition_dipole_moment
As I have understood it, the interaction of an atom with electric field causes a transition between its energy states, and this gives the atom a dipole moment ("transition dipole moment"). But it is this dipole moment that interacts which the electric field. This reasoning seems circular.
Moreover, before the transition is made, the dipole moment of the atom is zero. So how the interaction, which causes the transition, is possible in the first place? Or I have completely misunderstood this concept?
When an atom or molecule interacts with an electromagnetic wave of frequency
https://en.wikipedia.org/wiki/Transition_dipole_moment
As I have understood it, the interaction of an atom with electric field causes a transition between its energy states, and this gives the atom a dipole moment ("transition dipole moment"). But it is this dipole moment that interacts which the electric field. This reasoning seems circular.
Moreover, before the transition is made, the dipole moment of the atom is zero. So how the interaction, which causes the transition, is possible in the first place? Or I have completely misunderstood this concept?