- #1
NasuSama
- 326
- 3
Homework Statement
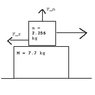
Small block 1 with mass m = 2.56 kg sits on top of large block 2 of mass M = 7.7 kg, and the pair sit on a frictionless, horizontal table. Between the blocks: the coefficient of kinetic friction is μk = 0.146, and the coefficient of static friction is μ_s = 0.203.
Find the magnitude of the maximum force applied horizontally to the upper block (block 1) that will cause the two blocks to slide together.
Homework Equations
Some ideas I have are:
→Σ F_up = Σ F_down
→Σ F_left = Σ F_right
→F = ma [Obviously]
→F_r = µ_k * F_N
The Attempt at a Solution
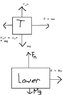
Just the free body diagram. See attached file. I am not sure about the down vertical component. I know that mg must point down, but what about the big M? Does that play the significant role for such problem?
I can't seem to find the next correct steps here.