- #1
MathematicalPhysicist
Gold Member
- 4,699
- 371
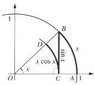
i am familiar to the this limit:
[tex]\lim_{x\rightarrow 0} sin(x)/x=1[/tex]
my question is does cosine,tg and cot have a similar idnetity limit or it's only a special case only in sine function?
[tex]\lim_{x\rightarrow 0} sin(x)/x=1[/tex]
my question is does cosine,tg and cot have a similar idnetity limit or it's only a special case only in sine function?