- #1
cowmoo32
- 122
- 0
Trouble with particular solution of differential equation - [SOLVED]
Find the particular solution of the differential equation

satisfying the initial condition
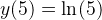
[STRIKE]I end up with (1/2)ln(-x^2+10x) which does satisfy the initial conditions, yet it's coming back as incorrect. Is there another way I can write the formula?[/STRIKE]
I figured it out, check post #3
Homework Statement
Find the particular solution of the differential equation
satisfying the initial condition
The Attempt at a Solution
[STRIKE]I end up with (1/2)ln(-x^2+10x) which does satisfy the initial conditions, yet it's coming back as incorrect. Is there another way I can write the formula?[/STRIKE]
I figured it out, check post #3
Last edited: