Two AC Sources with One Transformer

[Danksa]

I want to program a little power grid game and have the problem of connecting things via transformers. Imagine the following setup:

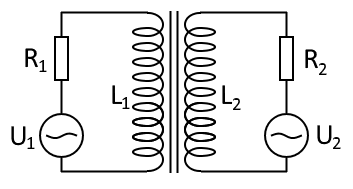
You can see the AC voltage sources as generators (or together with the resistor as a "consumer", if the amplitude is 0).

What I need to figure out are the Voltages across the inductors L1 and L2 and the currents which flow through the resistors R1 and R2. So the only things given are U1(t), R1, L1, U2(t), R2 and L2. What I already know is that the voltage across resistor R1 is:
U_{R1} = U_{L1} - U_1
the same thing goes for the voltage across R2:
U_{R2}=U_{L2}-U_2

Through some research I also found that the voltage across an inductor is given by:
U_{L1}=L_1 \cdot \frac{dI_1}{dt}+ M \cdot \frac{dI_2}{dt}

From that we can conclude that:
U_{R1}=L_1 \cdot \frac{dI_1}{dt} + M \cdot \frac{dI_2}{dt} - U_1
which is equavilent to:
I_1 = \frac{L_1}{R_1} \cdot \frac{dI_1}{dt} + \frac{M}{R_1} \cdot \frac{dI_2}{dt} - \frac{U_1}{R_1}
and for the other side:
I_2 = \frac{L_2}{R_2} \cdot \frac{dI_2}{dt} + \frac{M}{R_2} \cdot \frac{dI_1}{dt} - \frac{U_2}{R_2}

Where M = \sqrt{L_1 \cdot L_2} is the mutual inductance.

The problem is, that this differential equation seems to be highly unstable in a simulation (using numerical differentiation). Is there any solution to that? Just having one side without the other, so setting M=0 works just fine, but with both sides everything just "explodes".

Hopefully someone can help me :D

 

[anorlunda]

You can find what you need here https://en.wikipedia.org/wiki/Transformer#Ideal_transformer
The trick is this

the apparent load impedance referred to the primary circuit is derived in eq. (7) to be equal to the turns ratio squared times the secondary circuit load impedance.

Then you put the referred impecance in series with R1, completely removing the transformer from the circuit.

Be sure that you can control the phase angles of the two AC sources. Also do all your calculations in complex arithmetic, because you need to calculate real and imaginary voltages, currents and power (P=watts Q=VARS)

Good luck, what you're doing is good self-education.

 

[anorlunda]

Whoops. I forgot to mention that you should not think of that transformer as two inductors. Again, that Wikipedia article explains more.

 

[Danksa]

Hmm, I'll try this and see if it works, but I have a concern: if U1 is larger than U2 and both are in phase, then wouldn't power from the left side be transferred to the right? If R1 = R2? This can't be modeled with additional impedance, can it? I thought of replacing the inductor with impedance and an additional AC source, but I can't work that out either.

I guess I have to first look into the complex arithmetic stuff. I'm familar with complex numbers, but not too much with electronics (yet).

 

[anorlunda]

Power can flow either direction depending on the phase angles. If fact, phase angle is the dominant factor, not R or L. Try reading these two PF insights articles.

https://www.physicsforums.com/insights/ac-power-analysis-part-1-basics/
https://www.physicsforums.com/insights/ac-power-analysis-part-2-network-analysis/