. Arctic.
- 13
- 0
Homework Statement
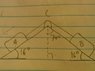
Blocks A and B are connected by a cable that passes over support C. Friction between the blocks and the inclined surfaces may be neglected. Knowing that motion of block B up the incline is impending when mB = 4.5 kg, determine:
(a) the coefficient of static friction between the rope and the support
(b) the largest value of mB for which equilibrium is maintained
Homework Equations
T2 = T1e^(μsβ) (1)
β is in angle in radians
W = mg
The Attempt at a Solution
My problem is that for part (b), my answer is wrong. I would like to know where I went wrong in my calculations. Thanks for the help in advance.
I found the forces working on Block A
ƩFx = 0
→ TA - WAsin(16) = 0
TA = 24.336 N
Then, Block B
ƩFx = 0
→ WBsin(16) - TB = 0
TB = 12.168 N
Then, I looked at support C where I found the angle to be 32°, and I used (1) to find the static friction.
β = (32)(∏/180) ≈ 0.559
TA = TBe^(μsβ)
24.336 N = (12.168 N)e^(μsβ)
e^(μsβ) = (24.336 N)/(12.168 N)
μsβ = ln [(24.336 N)/(12.168 N)]
μs = (1/0.559)*ln [(24.336 N)/(12.168 N)]
μs ≈ 1.240
Then, since I know TB has to be greater than itself to upset the equilibrium, I did
TB = TAe^(μsβ)
TB = (24.336 N)e^[(1.240)(0.559)]
TB ≈ 48.673 N
Then, to get the mass I divided the TB by g = 9.81
mB = (48.673)/(9.81) ≈ 4.962 kg
That is wrong.