Two Blocks on an Incline(picture)

[Dan350]

1. Would you correct, revise my problem please?

Two Blocks sit on a symmetric double slope. Rightmost block has twice the mass of the of the other block, and the angle that each side makes with the horizontal is the same.

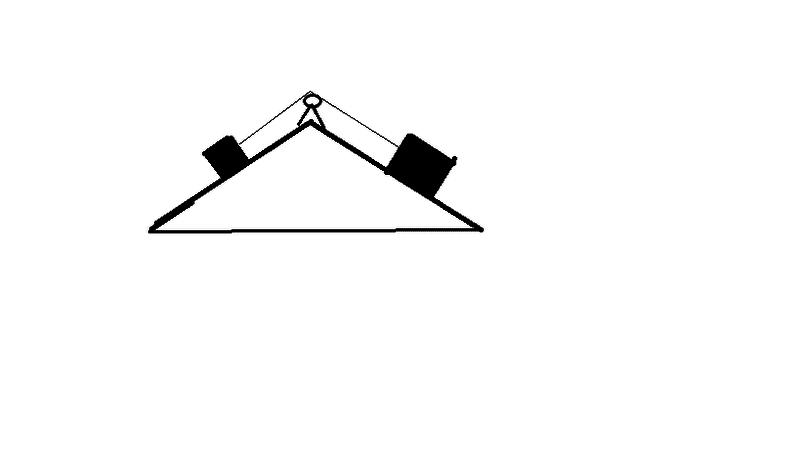
a) Suppose that there is no friction. and suppose that the slope angles are 25°, what is the acceleration of the blocks.

b)Suppose,again,that the slope angles are 25° and that there is no friction. Now suppose also that the tension rope is 100N. What is the mass of the smaller block?

c)Suppose again that there is no friction. Suppose that the slope angles are equal, but not necessarily 25. If the acceleration of the blocks is g/5. What are the slope angles?

d)For 25° angles, what is the minimum coefficient of friction for the blocks to remain stationary?




2.Newton's Second Laws



3. The Attempt at a Solution

a) Block A: ma= +T - mgsin@; Block B: 2ma= -T + 2mgsin@ adding the two equations,, tension cancels so, 3ma=mgsin@
I got 1.38m/s^2

b) for b i used my acceleration and the tension , then I solved for m, so T/(gsinθ+a)=m ; I got 18.11kg for the smaller block

c) I am lost in this one

d) for the coeffiecient,, I took my a,m, but only one side,, I used equation ma= +T - mgsin@-umgcosθ,,, I got .60 as the coeficient

 

[Panphobia]

For c) you have the mass ratio, you have acceleration, and the only unknowns are tension and the angle, but you have two equations. So two equations, two unknowns = solvable.

 

[haruspex]

There are three variables in each of a, b, and c: the angle, the mass ratio and the acceleration. From your equation, you can deduce any from the other two. The problem is that in c you only appear to be given one value. I think you need to assume the mass ratio is as given earlier - my guess is the 2:1 in a.
Same issue in d - you need to know the mass ratio. Please post more details of your working there.