Watagun
- 3
- 0
[Solved] Two Different Masses on an Uncentered Fulcrum (Torque)
Two blocks each of mass 1.9 kg are suspended from the ends of a rigid weightless rod of length l1 = 1.43 m and l2 = .085 m. The rod is held in the horizontal position shown and then released. Calculate the initial acceleration of the mass attached to l1. Assume up is positive and down is negative.
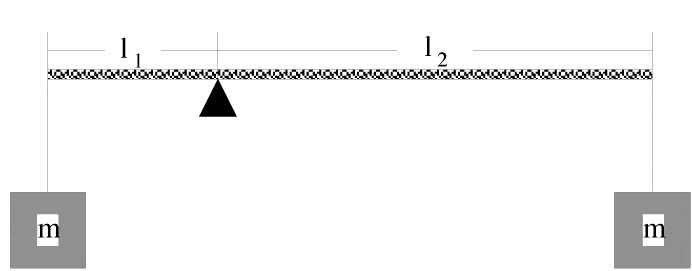
Also to clarify, the problem is asking for tangential acceleration
T = r x F
T = Ia
A = ar
I = mr2
First I summed the torque of the two sides
T = L1mg + L2mg = Ia
where mg is the force acting on the mass on each side and L1 and L2 are the radii.
For the moment of Inertia I, I used the point mass formula (I = mr2)
But that would apply for the system, so I added the two moment of Inertia for the two sides
I = mr12 + mr22
Doing some algebra to move the variables around I came up with
g(L1+L2)
----------- = a
(L12 + L22)
Putting in my numbers yielded me
9.8*(1.43+.085)/(1.432+.0852) = a = 7.23 rad/s2
Then after that I would need to divide 7.23 by the radius, r, to get the tangential acceleration. But I'm not sure which r I would use. r = L1? or r = (L1+L2)/2?
Anyway, that's what I came up with. I'm guessing there are a lot of mistakes in here, but I'm not sure what I did right and what I did wrong.
Any help pointing me in the correct direction would be great! :)
Homework Statement
Two blocks each of mass 1.9 kg are suspended from the ends of a rigid weightless rod of length l1 = 1.43 m and l2 = .085 m. The rod is held in the horizontal position shown and then released. Calculate the initial acceleration of the mass attached to l1. Assume up is positive and down is negative.
Also to clarify, the problem is asking for tangential acceleration
Homework Equations
T = r x F
T = Ia
A = ar
I = mr2
The Attempt at a Solution
First I summed the torque of the two sides
T = L1mg + L2mg = Ia
where mg is the force acting on the mass on each side and L1 and L2 are the radii.
For the moment of Inertia I, I used the point mass formula (I = mr2)
But that would apply for the system, so I added the two moment of Inertia for the two sides
I = mr12 + mr22
Doing some algebra to move the variables around I came up with
g(L1+L2)
----------- = a
(L12 + L22)
Putting in my numbers yielded me
9.8*(1.43+.085)/(1.432+.0852) = a = 7.23 rad/s2
Then after that I would need to divide 7.23 by the radius, r, to get the tangential acceleration. But I'm not sure which r I would use. r = L1? or r = (L1+L2)/2?
Anyway, that's what I came up with. I'm guessing there are a lot of mistakes in here, but I'm not sure what I did right and what I did wrong.
Any help pointing me in the correct direction would be great! :)
Last edited: