Two Leaning Sticks (Torque Calculation)

[Matt Raj]

Homework Statement

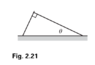
One stick leans on another as shown in Fig. 2.21. A right angle is formed where they meet, and the right stick makes an angle θ with the horizontal. The left stick extends infinitesimally beyond the end of the right stick. The coefficient of friction between the two sticks is μ. The sticks have the same mass density per unit length and are both hinged at the ground. What is the minimum angle θ for which the sticks don’t fall? (From Introduction to Classical Mechanics by David Morin)

Relevant Equations

N = (Mg/2) sin θ
F_f = (mg/2)cosθ

I attempted this problem trying to balance torques but I couldn't because the length of the left stick is unknown. From the right stick I got that mg/2* cos θ = F_f but from the left stick I got that Mg/2sin θ =N* r where r is the ratio of the length of where the sticks meet and the total length of the left stick. I looked at the answer and it didn't involve any ratio as such; in fact, the equation from the left stick provided in the solution was N = (Mg/2) sin θ. I'm confused why the solution didn't incorporate the length of the stick for the normal force on the left stick. Besides that one equation, I can solve the rest of the problem.

Update: I solved the problem by finding r but I'd like to know how the book found the equation " N = (Mg/2) sin θ " whereas I got N*cot θ* l/L = Mgsin θ and had to do some extra work.

 

[TSny]

Update: I solved the problem by finding r but I'd like to know how the book found the equation " N = (Mg/2) sin θ " whereas I got N*cot θ* l/L = Mgsin θ and had to do some extra work.

What equation do you get if you set up the torque equation for the left stick with the origin at the lower end of the left stick?

(I'm not sure what l and L mean in your equation).

 

[PhanthomJay]

If the length of the large stick is L, by basic trig, the length of the short left stick is Ltan theta. Thus the weight of the long stick is mg, and the weight of the short stick is mg tan theta. Since half of the long sticks weight goes vertically to the joint, you can resolve it into it’s friction and normal force. Does that help? You must then solve for Theta. Without using numbers.

 

[Matt Raj]

What equation do you get if you set up the torque equation for the left stick with the origin at the lower end of the left stick?

(I'm not sure what l and L mean in your equation).

"l" is the length of the right stick. I mistakenly assumed that the length of the left stick was "L" when the problem stated that it was infinite. There's a normal force from the right stick that should yield N= "the torque from the weight of the right stick", but how do you get the side of the equation for the weight as the length of the left stick is infinite?EDIT: Read the problem again, it said infinitesimally not infinitely like I assumed; thanks for your help

 

[IamVector]

"l" is the length of the right stick. I mistakenly assumed that the length of the left stick was "L" when the problem stated that it was infinite. There's a normal force from the right stick that should yield N= "the torque from the weight of the right stick", but how do you get the side of the equation for the weight as the length of the left stick is infinite?EDIT: Read the problem again, it said infinitesimally not infinitely like I assumed; thanks for your help

can we take torque around right hinge and equate it with torque of friction ? well it worked out pretty well for me.