Esragoria
- 2
- 0
1a. Homework Statement
Hi all, I'm having quite a bit of problem on a physics question. I've seen some examples of this problem, but when I follow the suggestions and equations out, the answer I get back is wrong...
Anyways, here's the problem:
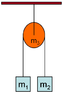
Given two masses (m_1,~m_2) hanging from opposite sides of a solid disk-shaped pulley of known mass and radius (m_3,~R) from a massless string, determine linear acceleration, angular acceleration of the pulley, the tension between the pulley and each of the two hanging masses and a few other things that I think I can work out on my own. I've attached a picture for reference.
I'd like to figure out how to solve this generally, but if it helps here are the masses and radii:m_1 = 3.6\text{ kg} m_2 = 1.7 \text{ kg} m_3 =2.2 \text{ kg} R = 0.15 \text{ m}
1b.
The variation replaces one of the masses with a sphere rolling without sliding on a flat surface. I've included a picture of this problem as reference. For this problem we are given the mass and radius of the sphere (m_s,~r_s), the mass and radius of the solid disk-shaped pulley (m_d,~r_d), and the mass and the radius of the hoop (which I have been treating as just a point mass because it appears to have no rotation) (m_h,~r_h).
Again, I'd like to figure this out generally, but here are the values given: $$m_s=3.2\text{ kg},~r_s=0.2\text{ m}$$ $$m_d=1.8\text{ kg},~r_d=0.09\text{ m}$$ $$m_h=2.4\text{ kg},~r_h=0.15\text{ m}$$
The equations I'm working with for 1a are: $$\vec{\tau}=\vec{R} \times \vec{F}= RT = I \alpha $$ $$a=R \alpha$$ $$I_\text{disk}= \frac{1}{2}mR^2$$
For 1b I'm also using: $$I_s= \frac{2}{5}mR^2$$
Assuming downward acceleration to be negative:
Additionally I have: $$\tau_\text{net}=I \alpha = RT_\text{net} = RT_1 - RT_2$$
Substituting in ##T_1 ,~ T_2,~\alpha=\frac{a}{R},~I_\text{disk}=\frac{1}{2}m_3 R^2 ##: $$\frac{1}{2}m_3 R^2 (\frac{a}{R}) = Rm_1 a + Rm_1 g - Rm_2 g - Rm_2 a$$
Simplifying out: $$a = 2g \frac{m_1 - m_2}{2m_2+m_3 - 2m_1}$$
and this is where I'm stuck. When I plug the numbers in, the online answer program is saying I'm wrong. I also simplified out using ##m_2 a=m_2g -T_2## resulting in: $$a = 2g \frac{m_1 - m_2}{m_3-2m_2 - 2m_1}$$ and ##T_1=m_1g-m_1a## resulting in: $$a = 2g \frac{m_1 - m_2}{m_3-2m_2 + 2m_1}$$ and these were both wrong
For 1b, I did essentially the same thing, except making down positive: $$\tau_s=I_s\alpha$$ $$\tau_h=R_dT_h$$ $$T_h=m_ha+m_h$$ $$\tau_\text{net}=\tau_s-\tau_h$$ Simplifying and substituting, I get: $$a=\frac{r_dm_hg}{\frac{2}{5}m_sr_s-r_d(m_h-\frac{m_d}{2})}$$ which is wrong.
Help would be appreciated!
Hi all, I'm having quite a bit of problem on a physics question. I've seen some examples of this problem, but when I follow the suggestions and equations out, the answer I get back is wrong...
Anyways, here's the problem:
Given two masses (m_1,~m_2) hanging from opposite sides of a solid disk-shaped pulley of known mass and radius (m_3,~R) from a massless string, determine linear acceleration, angular acceleration of the pulley, the tension between the pulley and each of the two hanging masses and a few other things that I think I can work out on my own. I've attached a picture for reference.
I'd like to figure out how to solve this generally, but if it helps here are the masses and radii:m_1 = 3.6\text{ kg} m_2 = 1.7 \text{ kg} m_3 =2.2 \text{ kg} R = 0.15 \text{ m}
1b.
The variation replaces one of the masses with a sphere rolling without sliding on a flat surface. I've included a picture of this problem as reference. For this problem we are given the mass and radius of the sphere (m_s,~r_s), the mass and radius of the solid disk-shaped pulley (m_d,~r_d), and the mass and the radius of the hoop (which I have been treating as just a point mass because it appears to have no rotation) (m_h,~r_h).
Again, I'd like to figure this out generally, but here are the values given: $$m_s=3.2\text{ kg},~r_s=0.2\text{ m}$$ $$m_d=1.8\text{ kg},~r_d=0.09\text{ m}$$ $$m_h=2.4\text{ kg},~r_h=0.15\text{ m}$$
Homework Equations
The equations I'm working with for 1a are: $$\vec{\tau}=\vec{R} \times \vec{F}= RT = I \alpha $$ $$a=R \alpha$$ $$I_\text{disk}= \frac{1}{2}mR^2$$
For 1b I'm also using: $$I_s= \frac{2}{5}mR^2$$
The Attempt at a Solution
Assuming downward acceleration to be negative:
##F_\text{net},_1 = m_1 a = T_1 - m_1 g ## resulting in a negative acceleration for ##m_1##
##F_\text{net},_2 = m_2 a = T_2 - m_2 g ## resulting in a positive acceleration for ##m_2##
Solving both for tension, I get: $$T_1=m_1a+m_1g$$ and $$T_2=m_2a+m_2g$$Additionally I have: $$\tau_\text{net}=I \alpha = RT_\text{net} = RT_1 - RT_2$$
Substituting in ##T_1 ,~ T_2,~\alpha=\frac{a}{R},~I_\text{disk}=\frac{1}{2}m_3 R^2 ##: $$\frac{1}{2}m_3 R^2 (\frac{a}{R}) = Rm_1 a + Rm_1 g - Rm_2 g - Rm_2 a$$
Simplifying out: $$a = 2g \frac{m_1 - m_2}{2m_2+m_3 - 2m_1}$$
and this is where I'm stuck. When I plug the numbers in, the online answer program is saying I'm wrong. I also simplified out using ##m_2 a=m_2g -T_2## resulting in: $$a = 2g \frac{m_1 - m_2}{m_3-2m_2 - 2m_1}$$ and ##T_1=m_1g-m_1a## resulting in: $$a = 2g \frac{m_1 - m_2}{m_3-2m_2 + 2m_1}$$ and these were both wrong
For 1b, I did essentially the same thing, except making down positive: $$\tau_s=I_s\alpha$$ $$\tau_h=R_dT_h$$ $$T_h=m_ha+m_h$$ $$\tau_\text{net}=\tau_s-\tau_h$$ Simplifying and substituting, I get: $$a=\frac{r_dm_hg}{\frac{2}{5}m_sr_s-r_d(m_h-\frac{m_d}{2})}$$ which is wrong.
Help would be appreciated!