Two torqued and hanging constrained rods

[pc100]

Homework Statement

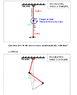
This is a general situation that I'm trying to figure out. Say there are two massless rods connected with a revolute joint, and one of the rods' other free end is connected to the wall with a free pin joint. There are two point masses in the system (see attachment), so the system is in a double pendulum configuration.

Now a torque τ appears between the rods only. What are the equations describing the motion of the two masses?
There's no gravity (i.e. this is sideways in a plane, for example)

Intuitively both the bottom and top masses will rotate and displace around some pseudo-center-of-mass point (the green dot P?), and with different displacements. I drew this guess onto the figure as well.

Homework Equations

These are not correct:
τ = I(m2 about P)*α(m2)
where I(m2 about P) = m2 * r(b to P)^2
and
τ = I(m1 about P)*α(m1)
where I(m1 about P) = m1 * r(a to P)^2

The Attempt at a Solution

The problem is that the wall is causing some strange behavior of the system, and I don't know how to approach this in closed form due to the constraint of the wall... Hints?

 

[radou]

How exactly is the constraint at point b (mass m2) defined?

 

[pc100]

This is a planar mechanism with two revolute joints whose axes are parallel to each other, and perpendicular to the plane defined by the ground and rods. So this rod setup can swing and bend side to side in the plane of the drawing. The constraint in the setup is the pin joint on one end of Rod 1 that keeps the mechanism connected to the wall.
So point b can slide around in the plane of the drawing, but aside from that, it has no constraint. For example, if point 'a' were held in place, then point 'b' would orbit around point 'a' in the plane of the drawing.