Two unknowns in trigonometric calculation?

[Ricaoma]

Hah, nevermind, I found a way to find x and then I could just insert the value to get v, just like I thought!

Homework Statement

A boat leaves the harbor going 60 degrees north-east with the speed 20km/h. 3 hours later, another boat leaves a harbor 160km to the east with a speed of 70km/h. What course should the second boat have to meet the first?

Homework Equations

Not 100% sure what equations would be relevant, but those who've crossed my mind have been:

The definitions of sine, cosine, tangent
$$\sin A = \frac{opposite}{hypotenuse}$$
$$\cos A = \frac{adjacent}{hypotenuse}$$
$$\tan A = \frac{opposite}{adjacent}$$

Law of sines
$$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$$

Law of cosines
$$c^2 = a^2 + b^2 - 2ab\cos C$$

Pythagorean theorem
$$a^2 + b^2 = c^2$$

Area
$$A = \frac{a*b*\sin C}{2}$$

The Attempt at a Solution

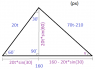
My sketched figure is attached to this post.

Start-phase
I started out by sketching a triangle with the base 160, the left side being 20t (20*time in hours since the first boat left) and the right being 70t-210 (70*time in hours since the first boat left - 70*3 for the 3 hours between the starting time).

Splitting the triangle
I also drew a line in the middle to make two right-angled triangles. Knowing that the bottom-left angle was 60 degees and that the new angle was 90 degrees I subtracted those two values from 180 to get the top angle of the left right-angled triangle.
$$180-(60+90) = 30$$

After that I used the definition of sine to calculate the length of the middle line, like this:
$$\sin60 = \frac{h}{20t}$$
$$20t * \sin60 = \frac{h}{20t} * 20t$$
$$20t * \sin60 = h$$

I did the same thing to find out the base of the left triangle:
$$\sin30 = \frac{b}{20t}$$
$$20t * \sin30 = \frac{b}{20t} * 20t$$
$$20t * \sin30 = b$$

With this knowledge I know that the base of the right-side triangle's base is
$$160 = 20t*sin(30) + b₂$$
$$160 - 20t * \sin30$$

The problem
I've tried all the things I've come up with so far, and most of them gives the same result. What I have to do is to get t out of any of the equations and then use that value to get rid of the t in all the equations. However, I have not yet been able to find an equation where this is an easy/possible task with my current trigonometric knowledge, which is pretty limited to the relevant equations listed above. Although, keep in mind that I may simply have missed an oppertunity to simplify an equation of overlooked some way of solving this, so the answer may still be in something that I think I've tried.

Some things I've tried:

Sine
$$\sin V = \frac{20t*\sin60}{70t-210}$$

Cosine
$$\cos V = \frac{160-20t*\sin30}{70t-210}$$

Law of Sine
Same result as my Sine-based approach
$$\frac{\sin90}{70t-210} = \frac{\sin V}{20t*\sin60}$$
$$\sin V = \frac{20t*\sin 60}{70t-210}$$

Law of Cossine
$$(20t)^2 = (70t-210)^2 + 160^2 - 2*160*(70t-210)*\cos V$$
$$\cos V = \frac{225t^2 - 1470t + 3485}{1120t - 3360}$$

Equation system based on area
Same result as my Sine-based approach
$$A = \frac{a*b*\sin V}{2}$$
$$A = \frac{a*h}{2}$$
$$\frac{a*b*\sin V}{2} = \frac{a*h}{2}$$
$$a*b*\sin V = a*h$$
$$b*\sin V = h$$
$$\sin V = \frac{h}{b}$$
$$\sin V = \frac{20t*\sin60}{70t-210}$$

Equation system based on Cosine and Law of Cosine
Don't know how to solve a third-degree equation like this
$$\cos V = \frac{160-20t*\sin30}{70t-210}$$
$$\cos V = \frac{225t^2 - 1470t + 3485}{1120t - 3360}$$
$$\frac{160-20t*\sin30}{70t-210} = \frac{225t^2 - 1470t + 3485}{1120t - 3360}$$
$$315t^3 - 2769t^2 + 6797t - 3885 = 0$$I'm really out of ideas now, so any ideas or thoughts are very much appreciated.

 

[Ricaoma]

Hah, nevermind, I found a way to find x and then I could just insert the value to get v, just like I thought!