Panphobia
- 435
- 13
Uncertainty partial derivatives
1 a) Give expressions for the uncertainty in both the area and volume of a right circular cone with radius R and height H and side length S. Assume that the radius has uncertainty σR and the height has an uncertainty σH. <----First part that I got.
b) For a radius R = 10.0 ± 0.1 cm and height H = 15.0 ± 0.2 cm, calculator the absolute uncertainty on both the area and the volume.
Surface area A = ∏*R^2 + (PI)*S*R
Volume V = (1/3)*∏*R^2*H
(S = sqrt(R^2 + H^2))
Ok so my attempt at solving this question was as follows
I tried to figure out the partial derivative with respect to the radius, and with respect to the height. When you get those the formula is
I was having trouble using the latex math equations thing so I just took a picture and here it is...
if it is unclear sigma and delta mean the same thing.
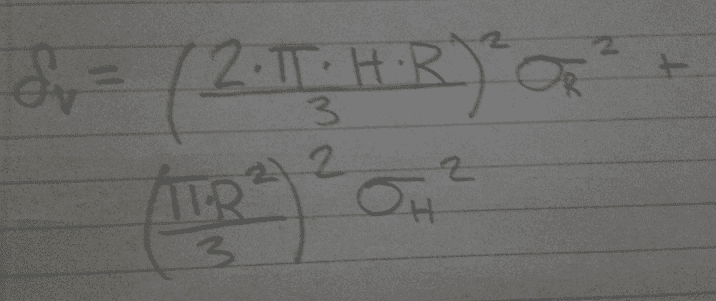
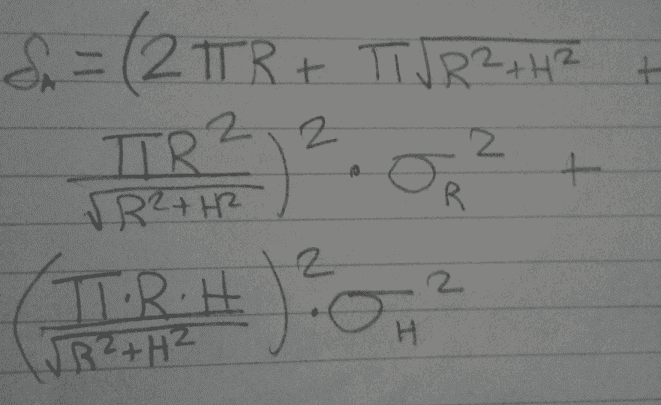
now I plugged in the values R = 10.0 ± 0.1 cm and height H = 15.0 ± 0.2 cm, and I got some absurdly high values, am I right, or did I do something wrong in my partial derivatives?
Homework Statement
1 a) Give expressions for the uncertainty in both the area and volume of a right circular cone with radius R and height H and side length S. Assume that the radius has uncertainty σR and the height has an uncertainty σH. <----First part that I got.
b) For a radius R = 10.0 ± 0.1 cm and height H = 15.0 ± 0.2 cm, calculator the absolute uncertainty on both the area and the volume.
Homework Equations
Surface area A = ∏*R^2 + (PI)*S*R
Volume V = (1/3)*∏*R^2*H
(S = sqrt(R^2 + H^2))
The Attempt at a Solution
Ok so my attempt at solving this question was as follows
I tried to figure out the partial derivative with respect to the radius, and with respect to the height. When you get those the formula is
I was having trouble using the latex math equations thing so I just took a picture and here it is...
if it is unclear sigma and delta mean the same thing.
now I plugged in the values R = 10.0 ± 0.1 cm and height H = 15.0 ± 0.2 cm, and I got some absurdly high values, am I right, or did I do something wrong in my partial derivatives?
Last edited:
 , so that explains a source of difference. My bad.
, so that explains a source of difference. My bad.