curiousnoncat
- 4
- 0
I'm a student taking a non-calculus strength of materials course, and I believe I have what is probably a very simple misconception.
I'm wondering why in the "eccentrically loaded column" b), which has two point loads placed at distances of equal magnitude from a centroidal axis, the moments will cancel each other out, and the cross section will be under uniform compression of a single value, but an element on beam a), which is in a state of plane stress, is not considered to be in compression in the y direction (at least in my textbook).
These seem completely analogous to me, besides the material's dimensions. I've got this sneaking suspicion that compression must exist in the y direction but is "negligible" (would it be negligible in an I-beam?), and also not uniformly distributed.
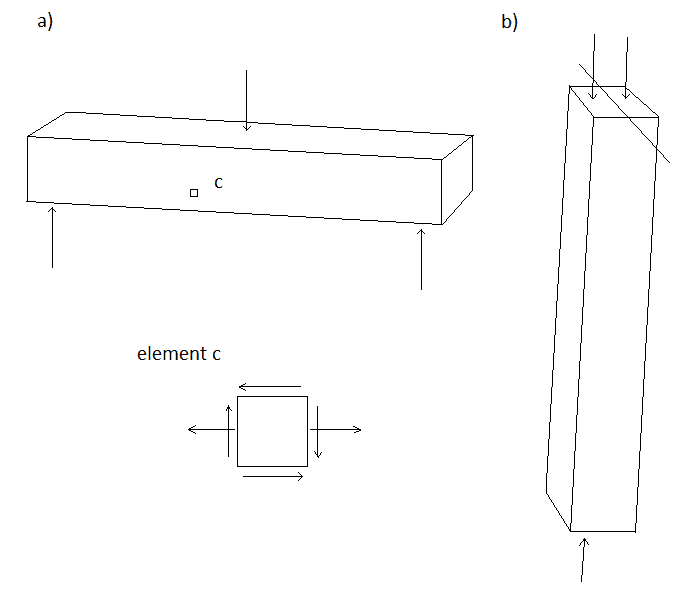
I'm wondering why in the "eccentrically loaded column" b), which has two point loads placed at distances of equal magnitude from a centroidal axis, the moments will cancel each other out, and the cross section will be under uniform compression of a single value, but an element on beam a), which is in a state of plane stress, is not considered to be in compression in the y direction (at least in my textbook).
These seem completely analogous to me, besides the material's dimensions. I've got this sneaking suspicion that compression must exist in the y direction but is "negligible" (would it be negligible in an I-beam?), and also not uniformly distributed.