Teachme
- 72
- 0
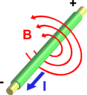
So I have a question about an electromagnet. I understand the right hand rule, and how the magnetic field wraps around the wire, but I don't understand the location of the north and south poles. How do you determine where the north and south poles are since the magnetic field is a circle around the wire? Thanks