umaza
- 10
- 0
I have two questions:
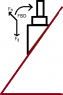
Pic 1: An object is placed on top of a spring scale which strapped to a horizontal surface. They slide down on an incline of 30 degrees. Friction is ignored. What fraction of the weight does the spring scale read of the top object? (Only incline is given, and friction is ignored)
Would the weight of the topmost object change at all? Would the topmost objects normal force be on an angle or still straight up because it is on a horizontal surface. Does acceleration affect weight at all?
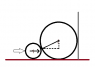
I drew what I thought the FBD would look like on the topmost object only including Normal force and weight, by this I think the weight is not affected.Pic 2: If there is an horizontal force, does the horizontal force go to the middle of the larger circle on an angle or does the force continue horizontally and only apply at the bottom of the larger circle? Also is it possible to lift the larger circle vertically with a horizontal force?
I drew what I thought would happen to the applied force horizontally.
Pic 1: An object is placed on top of a spring scale which strapped to a horizontal surface. They slide down on an incline of 30 degrees. Friction is ignored. What fraction of the weight does the spring scale read of the top object? (Only incline is given, and friction is ignored)
Would the weight of the topmost object change at all? Would the topmost objects normal force be on an angle or still straight up because it is on a horizontal surface. Does acceleration affect weight at all?
I drew what I thought the FBD would look like on the topmost object only including Normal force and weight, by this I think the weight is not affected.Pic 2: If there is an horizontal force, does the horizontal force go to the middle of the larger circle on an angle or does the force continue horizontally and only apply at the bottom of the larger circle? Also is it possible to lift the larger circle vertically with a horizontal force?
I drew what I thought would happen to the applied force horizontally.
Attachments
Last edited: