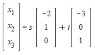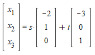Stephen Tashi said:
The function ##f## is a "linear operator", so that's my guess at the proper translation.
By convention, the matrix representation of a linear operator ##f## in a given basis is the matrix ##M## that satisifes:
##f(v) = Mv##
where the components of ##v## are those appropriate for the given basis. (i.e. The "matrix representation" employs matrix multiplication to implement the linear operator).
So my interpretation of the question is that its words pose two problems. These are:
1) Find the matrix ##M_a## that represents ##f## in the standard basis
2) Find the matrix ##M_b## that represents ##f## in the basis
##b_1 = \begin{bmatrix} 2 \\ -1 \\ 0 \end{bmatrix}, b_2 = \begin{bmatrix}3 \\ 0 \\ -1 \end{bmatrix}##.
However, perhaps you textbook is asking about a single matrix ##M## that somehow involves both bases.
What, precisely, is your interpretation of the question?
https://www.physicsforums.com/threads/how-to-use-latex-on-physics-forums.902358/
Straightfoward LaTex is somewhat verbose and tedious to write, but it's worth investing time to learn about it since it has applications outside of this particular forum. There are probably sophisticated ways to write LaTex concisely - I've never studied them.
Honestly I'm not sure at all. 99% of the time I cannot do an assignment, its because I simply don't understand what assignment is asking me to do. I find reading math notation very confusing, and Copenhagen University is notoriously inconsistent in use of notation from subject to subject. Basically my understanding is that it makes a matrix, which takes a 3 dimensional vector, as expressed in a 2 dimensional coordinate system (this is where I'm getting lost), and output a 2 dimensional vector, which is basically the 3 dimensional vector expressed in the standard basis, with the 3 coordinate removed.
PeroK said:
You have the correct ##A## matrix for ##f##. But, that matrix needs the input vector to be expressed in the normal basis. What the assignment wants is the matrix when the input vector is expressed in the new basis for ##U##.
Let's take a vector ##u \in U##. We can express this as:
##u = (s, t)_B## or ##u = (x_1, x_2, x_3)##
(I'll use this notation for now because it's easier than writing column vectors. I've used a subscript ##B## so it's clear which basis a vector is being expressed in.)
##u## is the same vector in both cases, so we know that:
##f(u) = f(s, t)_B = f(x_1, x_2, x_3) = (x_1, x_2)##
We can see from this that ##A## must be a 2x2 matrix. All we really need now is a relationship between ##(s, t)_B## and ##(x_1, x_2)##.
Can you see what that relationship is?
Alright so my understanding of what needs to be done is correct. However after that you lose me. ##u = (s, t)_B## or ##u = (x_1, x_2, x_3)## being the same makes no sense to me.
Example: given ##\pmatrix{5 \\ 2 \\ -3}## which is part of U, but is described in the standard basis ##\mathbb {R}^{3}##.
Its coordinates in the U basis is ##\pmatrix{2 \\ -3}##, that is the linear combination ##2*v_{1}+(-3)*v_{2}##
Now yes, these two describe the same vector, just in different basis, and if that is what you mean by them being the same, then alright. This still leaves me with the fact, that the question to me, seem to be asking for a matrix, which takes the ##\pmatrix{2 \\ -3}##, and exports ##\pmatrix{5 \\ 2}##. But if that is true, then I'm not inputting a 3 dimensional vector, but a 2 dimensional one. This is where I'm stuck, because I simply cannot reconcile what the assignment asking me to do, with what I'm getting to. Idd as you say, this transformation can be done, by using a 2x2 matrix, by combining the A matrix I wrote, with the basis matrix for U. I simply cannot understand how reading the assignment text, I'm suppose to understand it as being what it wants. I see it asking for a vector with 3 elements, described in the U basis, and as we can both agree, this doesn't make since.
I'd love to it, if you could tell me how this seems obvious to you, so that I don't get stuck on formulation in the future. Also as for the 2x2 matrix, if we disregard the fact that I cannot understand the assignment text, I say the matrix I'm looking for is $$\pmatrix{1 & 0 & 0 \\ 0 & 1 & 0}*\pmatrix{-2 & -3 \\ 1 & 0 \\ 0 & 1}=\pmatrix{-2 & -3 \\ 1 & 0}$$
PeroK said:
##U## is a 2 dimensional (2D) subspace (of a 3 dimensional vector space). ##U## can, therefore, be spanned by two basis vectors (as you have already done). The mapping from ##U## to ##\mathbb{R}^2## is simply a mapping from one 2D space to another.
Your question about the vectors in ##U## being "3 dimensional vectors" is an interesting one. This highlights that it's not actually the vectors that have a dimension but the vector space that has a dimension. Consider, for example, the x-, y- and z- axes in ##\mathbb{R}^3##. Are they three dimensional vectors? No. They are simply vectors. Each axis is a 1D subspace. It's only when you take all three axes together that you get a 3D vector space.
So, although we quite often talk about "3D vectors", vectors themselves don't actually have a dimension. Only the vector space has a dimension.
Maybe calling the vectors "X dimensional" is incorrect. Its merely my way of trying to convey what I mean :)
 upload_2017-12-30_16-35-10.png2.7 KB · Views: 372
upload_2017-12-30_16-35-10.png2.7 KB · Views: 372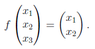 upload_2017-12-30_16-36-57.png1.8 KB · Views: 785
upload_2017-12-30_16-36-57.png1.8 KB · Views: 785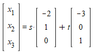 upload_2017-12-30_16-40-42.png812 bytes · Views: 379
upload_2017-12-30_16-40-42.png812 bytes · Views: 379 upload_2017-12-30_16-51-28.png368 bytes · Views: 394
upload_2017-12-30_16-51-28.png368 bytes · Views: 394 upload_2017-12-30_16-52-43.png479 bytes · Views: 374
upload_2017-12-30_16-52-43.png479 bytes · Views: 374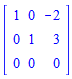 upload_2017-12-30_16-53-2.png421 bytes · Views: 369
upload_2017-12-30_16-53-2.png421 bytes · Views: 369