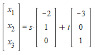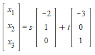- #1
NicolaiTheDane
- 100
- 10
Homework Statement
I have an assignment for my linear algebra class, that I simply cannot figure out. Its going to be hard to follow the template of the forum, as its a rather simply problem. It is as follows:
Given the following subspace (F = reals and complex)
and the "linear image" (cannot translate the wording here. Image is as close as I can get),
a) Find a basis for the subspace U ⊂ F^3
This part is easy enough. Just setup the equation as "parametric equation" (I have no idea if this is the right term. Its what google translate gives me), and the two resulting vectors, are the vectors that span the subspace:
b) Specify the A matrix, which represents f: U → F^2, in terms of the found basis for U and the standardbasis (e1,e2) for F^2
This is the one I cannot figure out. Using the two basis vectors for U, I can make a matrix which does the opposite; f : F^2 → U. However the assignment here wants me to go the opposite way, and I simply cannot figure out how to do this.
Homework Equations
Listed above
The Attempt at a Solution
Not really anything, because I have no idea how to go about it. The only I have noticed I can do, is take the two basis vectors as a matrix
Setup another vector from the subspace U, and gauss eliminate it as such:
That [-2,3] vector, if put back through the basis vector matrix, returns the [5,2,-3], as it should. So in essence I can make it happen backwards, but like I said, that isn't the assignment, and I simply don't know where to begin.
Thanks in advance for all assistance.
P.S How the hell do setup math nicely on this forum, so I can avoid using images in the future? :)
Attachments
-
 upload_2017-12-30_16-35-10.png2.7 KB · Views: 315
upload_2017-12-30_16-35-10.png2.7 KB · Views: 315 -
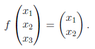 upload_2017-12-30_16-36-57.png1.8 KB · Views: 728
upload_2017-12-30_16-36-57.png1.8 KB · Views: 728 -
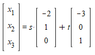 upload_2017-12-30_16-40-42.png812 bytes · Views: 321
upload_2017-12-30_16-40-42.png812 bytes · Views: 321 -
 upload_2017-12-30_16-51-28.png368 bytes · Views: 318
upload_2017-12-30_16-51-28.png368 bytes · Views: 318 -
 upload_2017-12-30_16-52-43.png479 bytes · Views: 296
upload_2017-12-30_16-52-43.png479 bytes · Views: 296 -
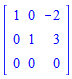 upload_2017-12-30_16-53-2.png421 bytes · Views: 316
upload_2017-12-30_16-53-2.png421 bytes · Views: 316