JC2000
- 186
- 16
- TL;DR
- Unable to put a finger on exactly why the following holds :
1. The voltage between the extreme nodes and central tap of the transformer is half of the voltage difference between the extreme nodes.
2. A 180 degree phase difference exists between the voltage at extreme nodes.
While trying to understand the working of a full wave rectifier I was unable to precisely understand the working of the central tap transformer.
Edit 1 : The voltages are out of phase by 180 degrees as voltage is alternating(?) So the only thing I don't understand is how the distribution of amplitudes occurs...
Thank you for your time!
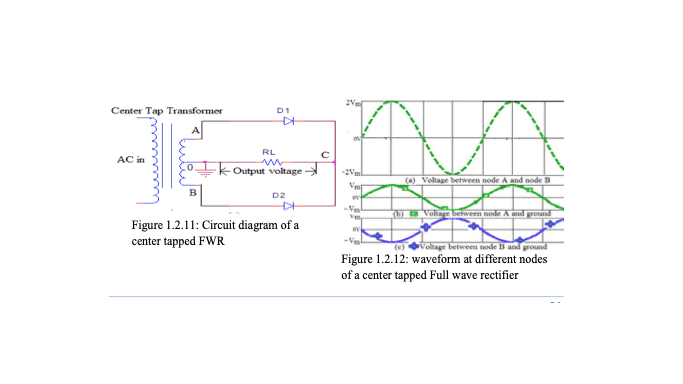
Edit 1 : The voltages are out of phase by 180 degrees as voltage is alternating(?) So the only thing I don't understand is how the distribution of amplitudes occurs...
Thank you for your time!
Last edited: