Understanding the Basics of Wave Phases for Beginners

[K41]

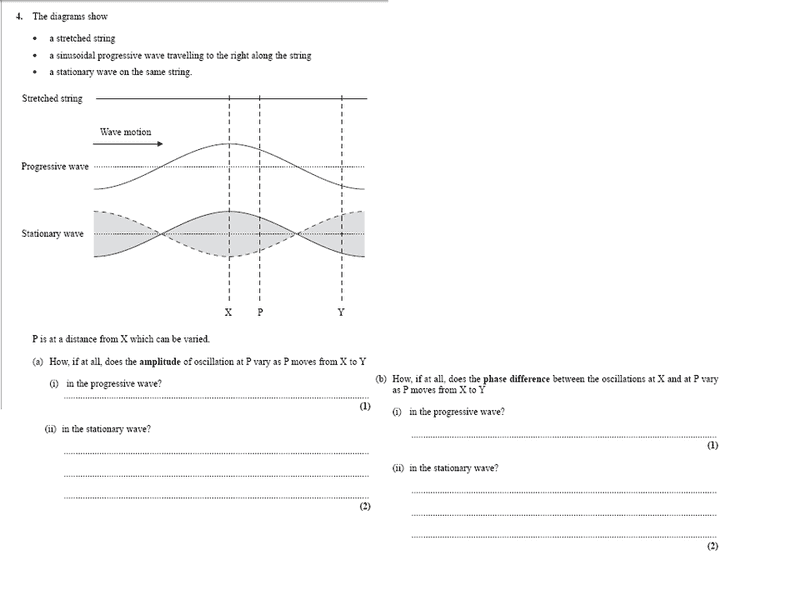
Wave Phases? Wtf?

Homework Statement

Homework Equations

None

The Attempt at a Solution

I managed to do the first part, but not the second part regarding phases. I don't have a clue how to work the second part out. I know that an anti-node is maximum amplitude and a node is at minimum amplitude. But I don't have a clue how to work out phases, nor do I understand what phase means or why it is used.

 

[Redbelly98]

Welcome to Physics Forums.

It may help to write out the general equation for oscillation at a fixed point:

y = A cos(ωt - φ)​

φ is the phase they are speaking of. The question is, essentially, does φ change as the point P moves from X to Y.