Understanding the Cauchy Stress Tensor: Clearing Up My Confusion

[Kushwoho44]

I have been trying to fully grasp the concept of the Cauchy stress tensor and so I thought I'd make a post where I clear up my confusion. There may be subsequent replies as I pose more questions.

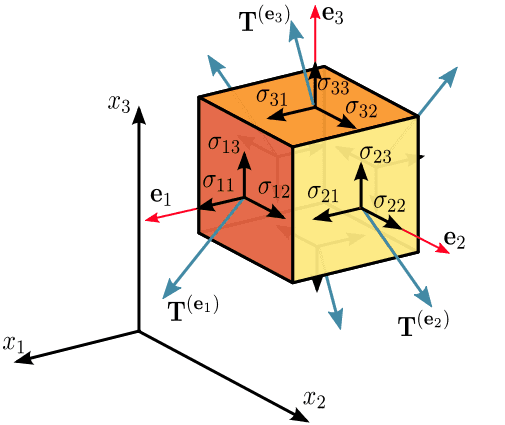
I am specifically confused at how the stress tensor relates to the control volume in the image above. My understanding has evolved to the conclusion: The stress tensor is defined at every point in the field, thus there would be a tensor defined at each point in the above control volume.

Questions: The control volume illustration above, though, seems to suggest that you can shrink the control volume to an infinitesimal element to where the stresses on that element will be described by the stress tensor. This is fine, but I cannot seem to understand how the stresses on the 'hidden' faces are included in the tensor? In the case of a fluid flowing, we cannot assume static condition and deduce that they are necessarily equal and opposite to the stresses on the 'front' faces?

Kind regards.

 

[Orodruin]

The stress tensor has nothing to do with the forces on a volume. It has to do with the force across a surface. Since it is a rank 2 tensor, it describes a linear map from vectors (the directed area element) to vectors (the force on an area element).

 

[Chestermiller]

To add to what Orodruin said, which, incidentally is a much better way of looking at the application of the stress tensor, I would also say that the forces on the area elements on the hidden faces (exerted by the surrounding fluid on the control volume) can differ (a small amount) from those on the exposed faces. This results in an actual force balance on the control volume.

 

[Kushwoho44]

The stress tensor has nothing to do with the forces on a volume. It has to do with the force across a surface. Since it is a rank 2 tensor, it describes a linear map from vectors (the directed area element) to vectors (the force on an area element).

To add to what Orodruin said, which, incidentally is a much better way of looking at the application of the stress tensor, I would also say that the forces on the area elements on the hidden faces (exerted by the surrounding fluid on the control volume) can differ (a small amount) from those on the exposed faces. This results in an actual force balance on the control volume.

Orodruin, ChesterMiller, thanks for your responses. A follow-up:

So, would I be correct to say that on each face in the illustrated control volume, there would be one normal stress and two shear stress components to the force on that area element. This is a special case as the face is normal to the reference axis. However, if we were to 'slice' and examine a face that is not normal to any of the reference axis, we would see that on this surface, there are 6 components to the force, three normal stresses, three shear stresses?

Further, I have seen it written that $\tau_xy = \tau_yx$ because of static equilibrium and the consequent need for angular momentum to be balanced. But in a fluid element, why is this still the case? The element could be rotating and I cannot see it demanded that $\tau_xy = \tau_yx$.

Kind regards,

Kush
Mentor: fix latex

 

[Orodruin]

However, if we were to 'slice' and examine a face that is not normal to any of the reference axis, we would see that on this surface, there are 6 components to the force, three normal stresses, three shear stresses?

No, definitely not. A force is a vector and has 3 components. The force on an infinitesimal surface element $d\vec S$ is given by $d\vec F = \sigma \cdot d\vec S$ and integrating this over an entire surface of a volume gives the total surface force on that volume.

 

[Orodruin]

However, the force across a surface depends on the orientation of the surface. Hence, the stress tensor has 6 independent components.

 

[Kushwoho44]

No, definitely not. A force is a vector and has 3 components. The force on an infinitesimal surface element $d\vec S$ is given by $d\vec F = \sigma \cdot d\vec S$ and integrating this over an entire surface of a volume gives the total surface force on that volume.

Hi, apologies, the '6' forces was a typo.

Yes, I do think I have a clear picture now. So, at each point in space, there are six components of stress (3 shear, 3 normal). If we are interested in the forces/stresses on a surface, we take the dot product of the area/normal vector to get the result we are after.

However, I still don't quite understand the second part of my questions:

Further, I have seen it written that $\tau_xy = \tau_yx$ because of static equilibrium and the consequent need for angular momentum to be balanced. But in a fluid element, why is this still the case? The element could be rotating and I cannot see it demanded that $\tau_xy = \tau_yx$.

 

[Chestermiller]

Further, I have seen it written that $\tau_xy = \tau_yx$ because of static equilibrium and the consequent need for angular momentum to be balanced. But in a fluid element, why is this still the case? The element could be rotating and I cannot see it demanded that $\tau_xy = \tau_yx$.

I may be mistaken, but I think this is required in order to be consistent with the stress tensor being proportional to the rate of deformation tensor (for a Newtonian fluid), while any rigid body rotations of the observer (or equivalently, rigid body rotational aspects of the fluid kinematics) are not mathematically allowed to contribute to the state of stress (since they do not constitute true deformation of the fluid).