flughafen
- 2
- 0
- Homework Statement
- statistics
- Relevant Equations
- pmf
I am new to the topic so I do need your help here. Thanks in advance
Understanding the PMF of a Random Variable: A Brief Overview
- Thread starter flughafen
- Start date
Join the discussion
Registration is free. Ask a follow-up in this thread, or start your own.
4 replies · 2K views
Discussion
- 16,219
- 4,934
Hello @flughafen, 
!
Unfortunately for you, PF requires an effort from you before we are allowed to assist. So: what have you got thus far ?
!Unfortunately for you, PF requires an effort from you before we are allowed to assist. So: what have you got thus far ?
flughafen
- 2
- 0
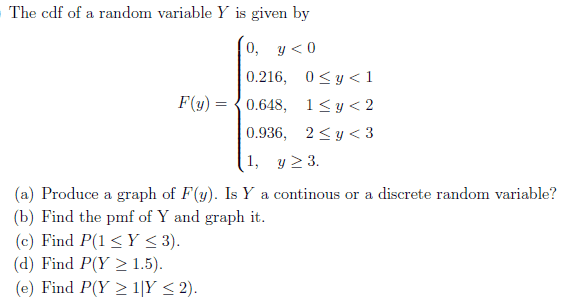
BvU said:Hello @flughafen,
Unfortunately for you, PF requires an effort from you before we are allowed to assist. So: what have you got thus far ?
I haven't gotten much far yet. Just left it there, thinking that I could use the answer of this as base for other alike questions.
etotheipi
flughafen said:
Have you tried sketching the cdf as in part a? This should help you to see what's going on.
Last edited by a moderator:
- 42,895
- 983
Do you not at least know the difference between a "continuous" and a "discrete" probability distribution? That is one of the questions asked that you did not answer.