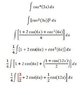Understanding the Power Reducing Identity in Trigonometric Functions

[mike01]

Homework Statement

See attached image

Homework Equations

Power reducing Identy:
cos^u = (1+Cos2u / 2)

The Attempt at a Solution

This is a problem that was done as an example (I know it is not complete it is missing the last integration step) but this is where I am getting stuck my question is where in this (3/2) coming from indicated in red in the image I cannot figure it out? thanks in advance.

 

[Mathnerdmo]

There's a 1 on the left side of the integrand, and a 1/2 coming from the fraction on the right.

1 + 1/2 = 3/2...

 

[mike01]

stupid question the 1/2, does that not stay with the second equation why would you inocrporate it into the first also??