I Units in Z_m .... Anderson and Feil, Theorem 8.6 .... ....

[Math Amateur]

I am reading Anderson and Feil - A First Course in Abstract Algebra.

I am currently focused on Ch. 8: Integral Domains and Fields ...

I need some help with an aspect of the proof of Theorem 8.6 ...

Theorem 8.6 and its proof read as follows:

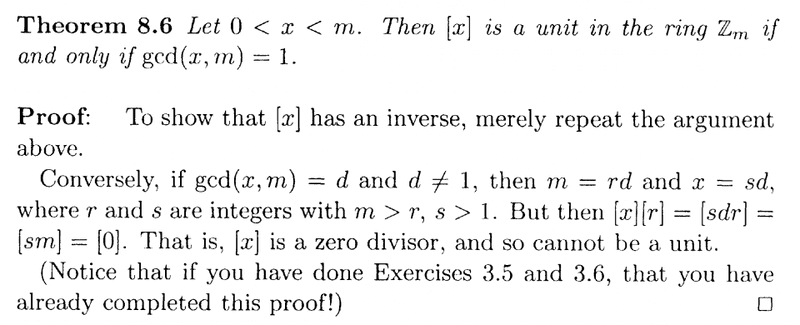
In the above text, Anderson and Feil write the following:

" ... ... Conversely, if $gcd(x,m) = d$ and $d \neq 1$, then $m = rd$ and $x = sd$, where $r$ and $s$ are integers with $m \gt r, s \gt 1$. ... ... "I cannot see exactly why/how $m \gt r, s \gt 1$ ... can someone help me to prove that $m \gt r$ and $s \gt 1$ ... ... ?
Help will be appreciated ...

Peter

 

[mathers101]

First off, you should note that the author doesn't mean to write $m>r$ and $s>1$. What he means is that $m>r>1$ and $m>s>1$.

Now, there is nothing fancy going on here. If $d=\gcd(x,m)$, then $d$ divides both $x$ and $m$, so we can write $m=rd$ and $x=sd$ for some integers $r,s$. Now, since we're assuming $d\neq1$, i.e. $d>1$, then we must have $r<m$ because if $r\ge m$, then we'd have $m=rd\ge md>m$, which is a contradiction. Similarly, $s<x$, and $x<m$ by assumption so $s<m$.

Now actually, I believe there is a typo here from the author. You don't necessarily need $s>1$, you could have $s=1$. Note the fact that $s>1$ isn't actually used in the rest of the proof, so it doesn't matter.

Edit: sorry for the poor formatting, this is my first time using this forum to answer a math question and I assumed it would use TeX commands.

 

[fresh_42]

Edit: sorry for the poor formatting, this is my first time using this forum to answer a math question and I assumed it would use TeX commands.

It does, but the syntax varies a bit from editor to editor. Here you have to use [\itex] or double # # for inline tex and [\tex] or double $ $ for single line tex. See &lt;a href=&quot;https://www.physicsforums.com/help/latexhelp/&quot; class=&quot;link link--internal&quot;&gt;https://www.physicsforums.com/help/latexhelp/&lt;/a&gt;

 

[Math Amateur]

Thanks mathers101 ... just worked through what you have said ...

Your argument is VERY clear and helpful ...

Thanks again ...

Peter

 

[Math Amateur]

Hi mathers101 ...

Just realized that I am unsure of where m > r > 1 is used in the rest of the proof ...

Can you help with this matter ...

Peter

 

[mathers101]

Hi mathers101 ...

Just realized that I am unsure of where m > r > 1 is used in the rest of the proof ...

Can you help with this matter ...

Peter

r > 1 is again not used at all, and r < m tells you that [r] is a nonzero element of Z_m, so since [x][r] = 0, we see [x] is a zero divisor.