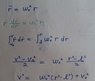athrun200
- 275
- 0
Homework Statement
Homework Equations
The Attempt at a Solution
In part a, there is an important step, I don't know how to have the step that written in green colour.
Does this technque have any name?
Can you give me more example of it?