gracy
- 2,486
- 83
<[/PLAIN] Mentor Note -- thread moved to HH from the technical math forums, so no HH Template is shown >[/color]
http://www.chilimath.com/flash-quiz/algebra/intermediate/oef/odd-even-functions-quiz.html
In this quiz I got all correct except 4th question.
I know how to figure out function is odd or even but for that I have to know the function of the graph I know equation of parabola is ##f(x)##=##x^2##
but I don't know whether it is applicable for upside down parabola,by upside down parabola I mean parabola of this type
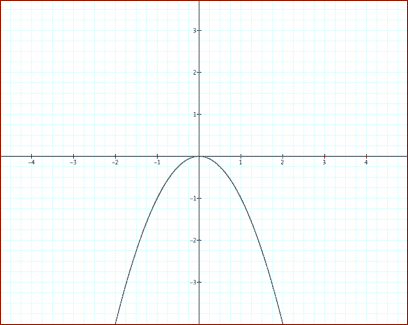
http://www.chilimath.com/flash-quiz/algebra/intermediate/oef/odd-even-functions-quiz.html
In this quiz I got all correct except 4th question.
I know how to figure out function is odd or even but for that I have to know the function of the graph I know equation of parabola is ##f(x)##=##x^2##
but I don't know whether it is applicable for upside down parabola,by upside down parabola I mean parabola of this type
Last edited by a moderator: