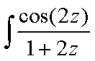You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Physics news on Phys.org
Pseudo Statistic
- 391
- 6
Two things.
1) Put this in the homework section, PLEASE!
2) For some reason your doc won't open with AbiWord. Care to paste it here?
1) Put this in the homework section, PLEASE!
2) For some reason your doc won't open with AbiWord. Care to paste it here?
bomba923
- 759
- 0
Why not just use \LaTeX ?
~
~
dextercioby
Science Advisor
- 13,390
- 4,045
Your integral is ugly enough not to be solved analytically. Since you're asked for an expression depending on "l" (and not for the antiderivative of the integrand), you could use a computer to see what it gives you.
Daniel.
Daniel.
benorin
Science Advisor
- 1,442
- 191
That's not pretty
\int \frac{\cos(2z)}{1+2z} dz = \frac{1}{2}\mbox{Si}(1+2z)\sin 1+\frac{1}{2}\mbox{Ci}(1+2z)\cos 1
where the functions Si(x) and Ci(x) are the Sine Integral and Cosine Integral functions (these are not elementary functions), respectively.
Alternatively, look here (Sine Integral) and here (Cosine Integral).
\int \frac{\cos(2z)}{1+2z} dz = \frac{1}{2}\mbox{Si}(1+2z)\sin 1+\frac{1}{2}\mbox{Ci}(1+2z)\cos 1
where the functions Si(x) and Ci(x) are the Sine Integral and Cosine Integral functions (these are not elementary functions), respectively.
Alternatively, look here (Sine Integral) and here (Cosine Integral).
quantumdude
Staff Emeritus
Science Advisor
Gold Member
- 5,560
- 24
lisawoods said:I have actually progressed with it now. The whole point was not to use a computer to solve it but to do it by hand.
I am now stuck on this bit any ideas? oh the integral is with respect to dz
Lisa,
It might expedite matters if you typed out your problems using LaTeX. Click on the image below to see the code that was used to generate it (won't work if you have a pop-up blocker on).
\int\frac{\cos(2z)}{1+2z}dz
Now I have two questions for you:
1.) Is that integral supposed to be definite, or indefinite?
2.) If it is definite, then are you familiar with the theory of residues? If it is indefinite, then I think you are doomed to either look it up in a table or use mathematical software.
lisawoods
- 9
- 0
Integral
its a definite integral with limits from 0 to L/2 where L is greater than 0.
How would you suggest I proceed with solving it using residues
Lisa
its a definite integral with limits from 0 to L/2 where L is greater than 0.
How would you suggest I proceed with solving it using residues
Lisa
quantumdude
Staff Emeritus
Science Advisor
Gold Member
- 5,560
- 24
Arrrgh...I was hoping that it went from -\infty to \infty because then a contour integral would be pretty straightforward, as your integrand only has one simple pole at z=-\frac{1}{2}.
I'll have to hit the books and review how to handle this. In the mean time, follow the lead given by benorin.
I'll have to hit the books and review how to handle this. In the mean time, follow the lead given by benorin.
lisawoods
- 9
- 0
Integral
Tom, did you get to talk to your math tutors?
Tom, did you get to talk to your math tutors?
Similar threads
- Replies
- 5
- Views
- 1K
- Replies
- 7
- Views
- 2K
- Replies
- 9
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 5
- Views
- 1K
- Replies
- 7
- Views
- 1K
- Replies
- 2
- Views
- 1K
- Replies
- 26
- Views
- 673
- Replies
- 6
- Views
- 1K
- Replies
- 1
- Views
- 2K
Hot Threads
-
Prove that the integral is equal to ##\pi^2/8##
- Started by Meden Agan
- Replies: 96
- Calculus and Beyond Homework Help
-
Solving the wave equation with piecewise initial conditions
- Started by songoku
- Replies: 11
- Calculus and Beyond Homework Help
-
Area of loop in x-y plane
- Started by littlemathquark
- Replies: 20
- Calculus and Beyond Homework Help
-
Solve this problem that involves induction
- Started by chwala
- Replies: 7
- Calculus and Beyond Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 92
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math