Fromaginator
- 8
- 0
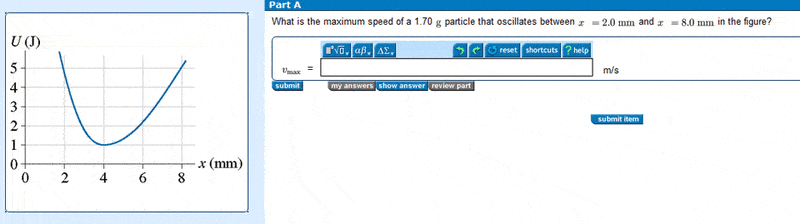
The Question
Relevant equations
KE=0.5*m*v^2
T=2*pi*sqrt(m/k)
EE=0.5*k*x^2
KEi+UEi=KEf+UEf
I think that's all of them
attempt at a solution
I was thinking about just using the conservation of energy at the the equilibrium point, as the kinetic energy would be at a max there and the potential energy would be at its minimum, Also the velocity would be at its max while the acceleration would be zero. However, one of the many problems I've run into on this question is that I'm unsure if the average of the two x values will give me the equilibrium point (if it did then it would be 5mm) and I don't feel comfrontable moving on having possibly made a false assumption.
Relevant equations
KE=0.5*m*v^2
T=2*pi*sqrt(m/k)
EE=0.5*k*x^2
KEi+UEi=KEf+UEf
I think that's all of them
attempt at a solution
I was thinking about just using the conservation of energy at the the equilibrium point, as the kinetic energy would be at a max there and the potential energy would be at its minimum, Also the velocity would be at its max while the acceleration would be zero. However, one of the many problems I've run into on this question is that I'm unsure if the average of the two x values will give me the equilibrium point (if it did then it would be 5mm) and I don't feel comfrontable moving on having possibly made a false assumption.