JohnSmith236
- 6
- 0
Homework Statement
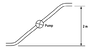
A pump is used to move water through a pipe of diameter 150mm, Figure below. The water has a temperature of 20 Celsius and an absolute pressure of 100KPa. The pump moves the water up a vertical distance of 2m and the water exists at atmospheric pressure.
Q1)
Assuming the process is adiabatic and friction less, and the required mass flow rate is ṁ= 2kg/s , determine, using the steady flow energy equation, the power required for the pump.
Q2)
Discuss how the effects of friction are accounted for by the steady flow energy equation. How would you introduce the effects of friction into the problem described above?
2. Homework Equations
0 = ∆H + ∆K.E.+ ∆P.E.
P = ṁ w
where
P = power (W)
ṁ = mass flow rate (kg/s)
w = specific work (Nm/kg, J/kg)
Specific work - w - can be expressed:
w = g h
where
h = head (m)
g = acceleration due to gravity (9.81 m/s2)
ṁ= ρ Q
where
ρ = density (kg/m3)
Q = volume flow rate (m3/s)
Power= ρ Q g h
The Attempt at a Solution
Q = ṁ/ρ
= 2/1000
=0.002
h= 2m ?? Not sure this answer is correct do not know the formula for head
P = ρ Q g h
= (1,000 kg/m3) (2*10-3 m3/s) (9.81 m/s2) (2)
= 4W
Attachments
Last edited: