Strand9202
- 10
- 2
- Homework Statement
- Velocity of an object: Picture of problem and work attached
- Relevant Equations
- Speed =s(t)
Acceleration = s'(t)
Velocity = s"(t) or a'(t)
Attached is the problem and my work through the problem. I got the problem correct, but my teacher said this could be done quicker on a calculator. Any idea how it could be done quicker.

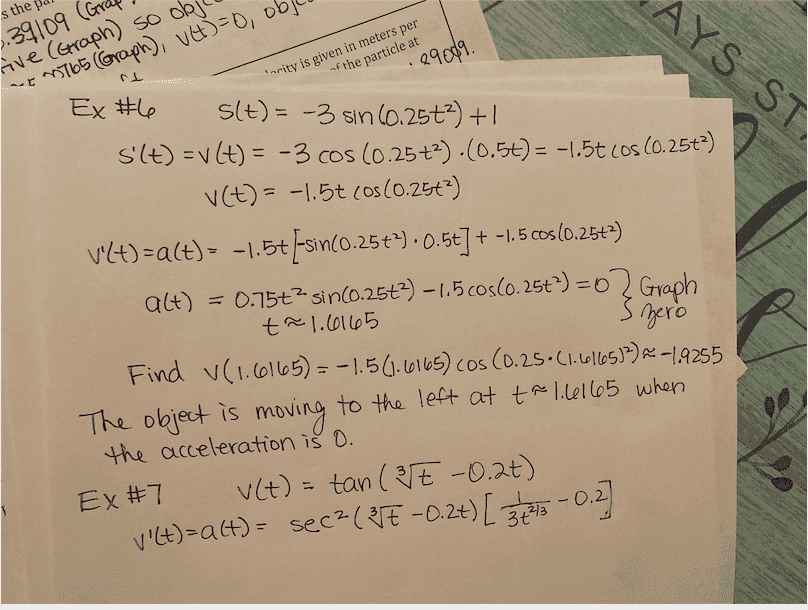
Attachments
Last edited:

