parmalesso
- 3
- 0
1. The problem is the following:
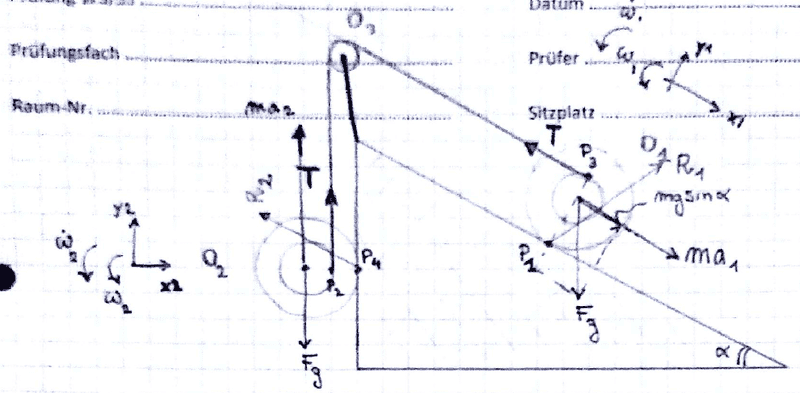
Starting from stillness @ t = 0, we are looking for the acceleration @T=0 of the 2 wheels (rolling without slip, in particular in point P4 we have a gear wheel contact so we can have that the reaction R2y of the plane could be also in direction y2, in this case, you can see that Reation R2x in direction x2 the reaction is 0).
The 2 wheels are connected with a not extendable Rope. Also Wheel 1 does not slip, so R1y = mgsin(alfa) with alfa = 30°, whereas R1x should be found.
the big radius of each wheel is R=20cm
The internal radius where the rope is rolled up is r = 10cm.
J of each wheel is 0.0125 kgm^2.
Weight of each wheel m = 1kg
domega1 = - a_o1 / R ; % Angle acceleration wheel 1 ( positive domega1 in clockwise direction)
domega2 = - a_o2 / R ; % Angle acceleration wheel 2 (positive domega2 in clockwise direction)
eq1 (Forces equilibrium direction x1) : m * g* sin(alfa) - T + R1x = m * a_o1 ;
eq2 (Momentum equilibrium around P1): ( J + m * R^2) * domega1 = T * (R+r) - m * g *sin(alfa) * R - m * a_o1 * R ;
eq3 (Forces equilibrium direction y2): - m * g + T + R2y = m * a_o2 ;
eq4 (Momentum equilibrium around P4) : ( J + m * R^2) * domega2 = m * g * R - m * a_o2 * R - T * (R-r) ;
eq5 (cynematic relationship) : domega2 * (R-r) = domega1 * (R+r) ;
Looking for:
a_01
a_02
T
R2y
R1x
I solve it with Matlab and i got a_02 about -23 m/s^2 which is in my opinion not acceptable.
What do i do wrong?
Thanks in advance!
Starting from stillness @ t = 0, we are looking for the acceleration @T=0 of the 2 wheels (rolling without slip, in particular in point P4 we have a gear wheel contact so we can have that the reaction R2y of the plane could be also in direction y2, in this case, you can see that Reation R2x in direction x2 the reaction is 0).
The 2 wheels are connected with a not extendable Rope. Also Wheel 1 does not slip, so R1y = mgsin(alfa) with alfa = 30°, whereas R1x should be found.
the big radius of each wheel is R=20cm
The internal radius where the rope is rolled up is r = 10cm.
J of each wheel is 0.0125 kgm^2.
Weight of each wheel m = 1kg
Homework Equations
domega1 = - a_o1 / R ; % Angle acceleration wheel 1 ( positive domega1 in clockwise direction)
domega2 = - a_o2 / R ; % Angle acceleration wheel 2 (positive domega2 in clockwise direction)
eq1 (Forces equilibrium direction x1) : m * g* sin(alfa) - T + R1x = m * a_o1 ;
eq2 (Momentum equilibrium around P1): ( J + m * R^2) * domega1 = T * (R+r) - m * g *sin(alfa) * R - m * a_o1 * R ;
eq3 (Forces equilibrium direction y2): - m * g + T + R2y = m * a_o2 ;
eq4 (Momentum equilibrium around P4) : ( J + m * R^2) * domega2 = m * g * R - m * a_o2 * R - T * (R-r) ;
eq5 (cynematic relationship) : domega2 * (R-r) = domega1 * (R+r) ;
The Attempt at a Solution
Looking for:
a_01
a_02
T
R2y
R1x
I solve it with Matlab and i got a_02 about -23 m/s^2 which is in my opinion not acceptable.
What do i do wrong?
Thanks in advance!