Vertical Load on a Purlin - find x and y force components

[KV-1]

A roof purlin, supported by a roof rafter must support a 300 lb vertical snow load.
Determine the component of of the snow load as a concentrated load “P” both perpendicular and parallel to the axis of the rafter.

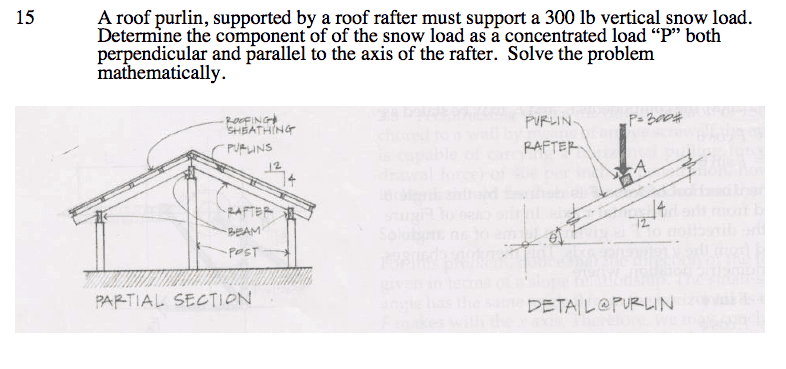I read that the perpendicular component of the 300lb force can be figured out by 300lb*cos(inverseTan(4/12)) and the parallel component can be figured out by 300lb*sin(18.43*)

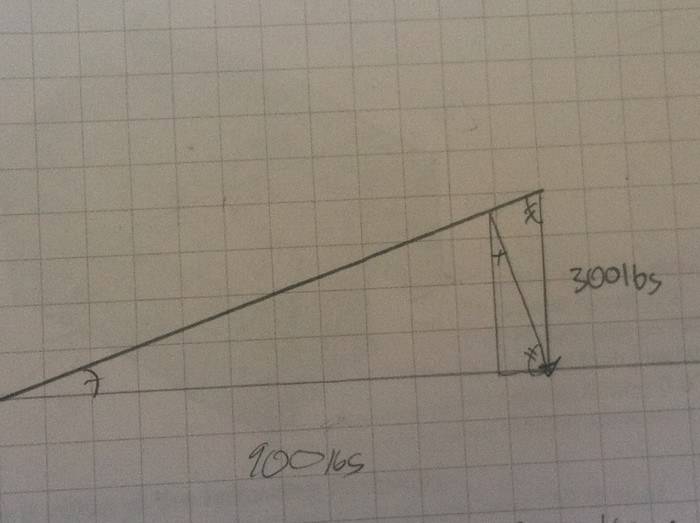
I do not understand why this is so. My attempt at the solution is to draw an FBD, but I suppose I am drawing the wrong one.

 

[SteamKing]

A free body diagram is nice, but what you really want to do is draw a triangle where the hypotenuse has a slope of 4:12 and then work out the angles normal and tangential to this slope. It's more a matter of geometry (and trigonometry) than anything else.