amolv06
- 45
- 0
Homework Statement
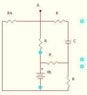
Below, I have attached a schematic that was on a test question for me. (NOTE: R4 = 4*r) We were supposed to find the current leaving the battery in terms of R, C, and Vb. The thing was, I had no idea what the voltage drop across the capacitor would be since there is no q given. How would one solve this?
Homework Equations
Kirchoff's laws
C=Q/V => V=Q/C
V=IR
The Attempt at a Solution
It's a bit hard showing since I would have a hard time drawing in all the loops and such, but I had 3 loops. I just didn't know what the equation for the one going through the top right would be since I'm not given q (or t).
I tried the following for the loop in question:
V_{b} - R(I_{2}+I_{3}) - IR_{3} - \frac{q}{c} - R(I_{3} + I_{1})=0