- #1
roam
- 1,271
- 12
I am looking for an explicit equation that shows that a sample with lesser volume will reach higher temperatures when irradiated than a sample with a larger volume.
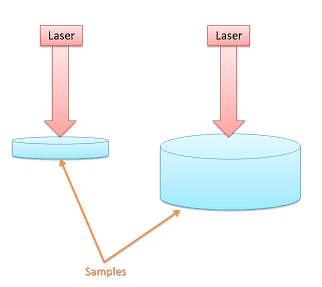
The samples in my project are biological tissues which are being irradiated by a laser. In my experiment, using a thermal camera I found that smaller samples (less volume) reached higher temperatures. Since water is the most abundant constituent, as a first-order approximation we could model the tissue as a volume of water. Here is a diagram I made:
If the sample has an initial temperature ##T_{i}## and final temperature ##T_{f}## and the temperature rise is ##\Delta T##, we can write:
$$T_{f}=T_{i}+\Delta T. \tag{1}$$
Therefore we need to show that ##\Delta T## decreases if the volume increases.
1. The only thing that my thermodynamics textbook states is that the heat capacity will be larger the more of a substance you have. But I really need the relationship between (solid) volume and temperature rise in the form of an explicit formula.
2. I have found an equation (source) that gives the value for ##\Delta T## for an irradiated sample:
$$\underbrace{E}_{\text{deposited energy}}=\underbrace{m}_{\text{mass}}\overbrace{c}^{\text{heat capacity}}\Delta T=\left(\underbrace{\rho}_{\text{density}}\overbrace{L}^{\text{height}}\underbrace{A}_{\text{beam area}}\right)c\Delta T. \tag{2}$$
However, they say that this is when the beam is absorbed in a distance of ##L## beneath the surface in a piece of material of mass ##m##. Therefore the volume that appears in the equation above (##LA##) is the volume in which the laser power is absorbed, not the overall volume of the material. I don't know how the overall volume comes into it...
3. The one-dimensional general heat conduction equation which gives the change in temperature over time at point a specific point in the tissue:
$$\frac{\partial T\left(z,\ t\right)}{\partial t}=K\ \frac{\partial^{2}T\left(z,\ t\right)}{\partial z^{2}}+\frac{Q\left(z,\ t\right)}{\rho c}. \tag{3}$$
This equation takes into account conduction (typically away from the irradiated spot) since the first term on the RHS describes heat conduction. The diffusivity is given by ##K=k/\rho c##. And ##Q## is the heat source term describing the rate at which heat is generated (this depends on the intensity of the laser and the absorptance of the material).
But how does the overall volume of the sample factor into this?
Any suggestions would be greatly appreciated.
The samples in my project are biological tissues which are being irradiated by a laser. In my experiment, using a thermal camera I found that smaller samples (less volume) reached higher temperatures. Since water is the most abundant constituent, as a first-order approximation we could model the tissue as a volume of water. Here is a diagram I made:
If the sample has an initial temperature ##T_{i}## and final temperature ##T_{f}## and the temperature rise is ##\Delta T##, we can write:
$$T_{f}=T_{i}+\Delta T. \tag{1}$$
Therefore we need to show that ##\Delta T## decreases if the volume increases.
1. The only thing that my thermodynamics textbook states is that the heat capacity will be larger the more of a substance you have. But I really need the relationship between (solid) volume and temperature rise in the form of an explicit formula.
2. I have found an equation (source) that gives the value for ##\Delta T## for an irradiated sample:
$$\underbrace{E}_{\text{deposited energy}}=\underbrace{m}_{\text{mass}}\overbrace{c}^{\text{heat capacity}}\Delta T=\left(\underbrace{\rho}_{\text{density}}\overbrace{L}^{\text{height}}\underbrace{A}_{\text{beam area}}\right)c\Delta T. \tag{2}$$
However, they say that this is when the beam is absorbed in a distance of ##L## beneath the surface in a piece of material of mass ##m##. Therefore the volume that appears in the equation above (##LA##) is the volume in which the laser power is absorbed, not the overall volume of the material. I don't know how the overall volume comes into it...
3. The one-dimensional general heat conduction equation which gives the change in temperature over time at point a specific point in the tissue:
$$\frac{\partial T\left(z,\ t\right)}{\partial t}=K\ \frac{\partial^{2}T\left(z,\ t\right)}{\partial z^{2}}+\frac{Q\left(z,\ t\right)}{\rho c}. \tag{3}$$
This equation takes into account conduction (typically away from the irradiated spot) since the first term on the RHS describes heat conduction. The diffusivity is given by ##K=k/\rho c##. And ##Q## is the heat source term describing the rate at which heat is generated (this depends on the intensity of the laser and the absorptance of the material).
But how does the overall volume of the sample factor into this?
Any suggestions would be greatly appreciated.