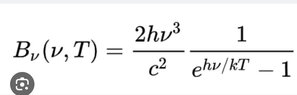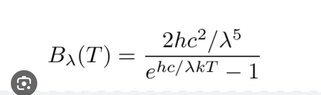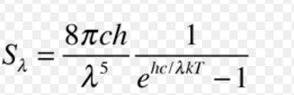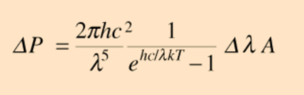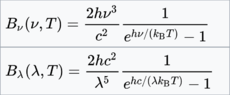sss1
- 50
- 2
- Homework Statement
- Below
- Relevant Equations
- In the pictures
Im getting confused between the differences of all of these formulas.
I googled spectral radiance black body and all of the first four pictures came up. They represent the intensity of radiation at a particular wavelength right, or the y-axis of the black body radiation curve? So if I integrate this formula I should get the total intensity? Or the total area under the black body radiation curve? One of the pictures has frequency as the variable instead of wavelength tho? Is it finding the same thing but for when I'm given frequency instead of wavelength? And somehow the rest of the three pictures all have different numerators...?
And the last formula, which finds the radiated power for a specific wavelength, why does it have a delta lambda in it? Kinda confused on where it comes about. I understand that spectral radiancy has units Watts/m^3, so it makes sense to have A and delta lambda, because that has units m^3. But why not have lambda instead of delta lambda? And also if i integrated that formula it will give me Stefan Boltzmann's law? The total power radiated?
I googled spectral radiance black body and all of the first four pictures came up. They represent the intensity of radiation at a particular wavelength right, or the y-axis of the black body radiation curve? So if I integrate this formula I should get the total intensity? Or the total area under the black body radiation curve? One of the pictures has frequency as the variable instead of wavelength tho? Is it finding the same thing but for when I'm given frequency instead of wavelength? And somehow the rest of the three pictures all have different numerators...?
And the last formula, which finds the radiated power for a specific wavelength, why does it have a delta lambda in it? Kinda confused on where it comes about. I understand that spectral radiancy has units Watts/m^3, so it makes sense to have A and delta lambda, because that has units m^3. But why not have lambda instead of delta lambda? And also if i integrated that formula it will give me Stefan Boltzmann's law? The total power radiated?
Attachments
Last edited: