m_physics
- 7
- 0
1. Problem:
The ground-state energy of a hypothetical atom is at -10.0eV. When these atoms, in the ground state, are illuminated with light, only the wavelengths of 207 nanometers and 146 nanometers are absorbed by the light atoms (1 nanometer = 10^-9meters).
(a)Calculate the energies of the photons of light of the two absorption-spectrum wavelengths.
(b)Complete the energy level diagram shown below for these atoms by showing all the excited energy states.
(c)Show by arrows on the energy-level diagram all of the possible transitions that would produce emission-spectrum lines.
(d)What would be the wavelength of the emission line corresponding to the transition from the second excited state to the first excited state?
E=13.6 [(1/ni^2)-(1/n2^2)]eV
En=-(13.6eV)[(Z^2)/(n^2)]
(1/λ)=(2pi^2mk^2e^4/h^3c)[(1/nf^2)-(1/ni^2)]
2pi^2mk^2e^4/h^3c = 1.097 x 10^7 m
E = hc/λ
hc=1.24 x 10^3eV
(a)
207nm = 2.07 x 10^-7m
146nm = 1.46 x 10^-7m
E = hc/λ
E1=[(1.24 x 10^3eV)/(2.07 x 10^-7)]
E1=5.99 x 10^9
E2=[(1.24 x 10^3eV)/1.46 x 10^-7)]
E2=8.493 x 10^9
(b)
I assumed it was bohr model...(?)
Ground state is at -10.0eV
First excited state is 1/4 of ground state
=(1/4)(-10.0eV)
first excited state=-2.5eV
Second excited state is 1/9 of ground state
=(1/9)(-10.0eV)
second excited state is -1.11eV
sorry about the terrible picture...
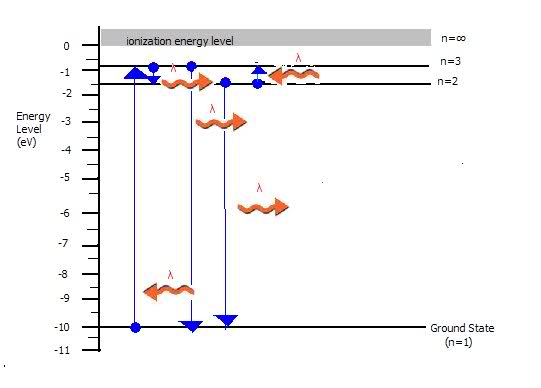
(c) is included in picture (?) squiggly arrows..
(d)
ni=2
nf=1
(1/λ)=(2pi^2mk^2e^4/h^3c)[(1/nf^2)-(1/ni^2)]
(1/λ)=(1.097 x 10^7 m)[(1/(1)^2)-(1/(2)^2)]
(1/λ)=(1.097 x 10^7 m)[(1/1)-(1/4)]
(1/λ)=(1.097 x 10^7 m)(1-0.25)
(1/λ)=(1.097 x 10^7 m)(0.75)
(1/λ)=8.2275 x 10^6
1=(8.2275 x 10^6)λ
λ=(1/8.2275 x 10^6)
λ=1.2154 x 10^-7m
The ground-state energy of a hypothetical atom is at -10.0eV. When these atoms, in the ground state, are illuminated with light, only the wavelengths of 207 nanometers and 146 nanometers are absorbed by the light atoms (1 nanometer = 10^-9meters).
(a)Calculate the energies of the photons of light of the two absorption-spectrum wavelengths.
(b)Complete the energy level diagram shown below for these atoms by showing all the excited energy states.
(c)Show by arrows on the energy-level diagram all of the possible transitions that would produce emission-spectrum lines.
(d)What would be the wavelength of the emission line corresponding to the transition from the second excited state to the first excited state?
Homework Equations
E=13.6 [(1/ni^2)-(1/n2^2)]eV
En=-(13.6eV)[(Z^2)/(n^2)]
(1/λ)=(2pi^2mk^2e^4/h^3c)[(1/nf^2)-(1/ni^2)]
2pi^2mk^2e^4/h^3c = 1.097 x 10^7 m
E = hc/λ
hc=1.24 x 10^3eV
The Attempt at a Solution
(a)
207nm = 2.07 x 10^-7m
146nm = 1.46 x 10^-7m
E = hc/λ
E1=[(1.24 x 10^3eV)/(2.07 x 10^-7)]
E1=5.99 x 10^9
E2=[(1.24 x 10^3eV)/1.46 x 10^-7)]
E2=8.493 x 10^9
(b)
I assumed it was bohr model...(?)
Ground state is at -10.0eV
First excited state is 1/4 of ground state
=(1/4)(-10.0eV)
first excited state=-2.5eV
Second excited state is 1/9 of ground state
=(1/9)(-10.0eV)
second excited state is -1.11eV
sorry about the terrible picture...
(c) is included in picture (?) squiggly arrows..
(d)
ni=2
nf=1
(1/λ)=(2pi^2mk^2e^4/h^3c)[(1/nf^2)-(1/ni^2)]
(1/λ)=(1.097 x 10^7 m)[(1/(1)^2)-(1/(2)^2)]
(1/λ)=(1.097 x 10^7 m)[(1/1)-(1/4)]
(1/λ)=(1.097 x 10^7 m)(1-0.25)
(1/λ)=(1.097 x 10^7 m)(0.75)
(1/λ)=8.2275 x 10^6
1=(8.2275 x 10^6)λ
λ=(1/8.2275 x 10^6)
λ=1.2154 x 10^-7m