Maskawisewin
- 3
- 0
What does "phase of the motion in terms of cosine displacement" mean?
I'm getting tripped up on the wording of this homework question.
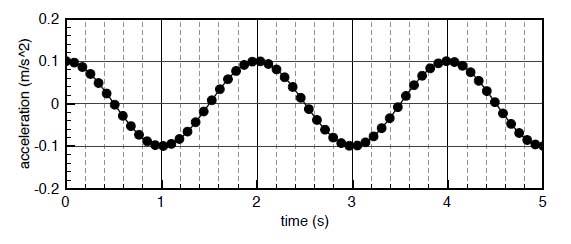
Measured acceleration: An accelerometer has measured the simple harmonic motion shown in the image below.
You want to describe the position as a function of time as a cosine: x(t)=A\cos(\omega t-\phi).
What is the phase of the motion shown in the graph (in terms of a cosine displacement)?
I've tried reading my textbook for "phase of the motion". There's a section that talks about a rotating vector phasor that references the unit circle. Is this the right path? Are they talking about what the cosine is calculating (i.e. what's inside the brackets of the cosine)?
I'm getting tripped up on the wording of this homework question.
Homework Statement
Measured acceleration: An accelerometer has measured the simple harmonic motion shown in the image below.
Homework Equations
You want to describe the position as a function of time as a cosine: x(t)=A\cos(\omega t-\phi).
What is the phase of the motion shown in the graph (in terms of a cosine displacement)?
The Attempt at a Solution
I've tried reading my textbook for "phase of the motion". There's a section that talks about a rotating vector phasor that references the unit circle. Is this the right path? Are they talking about what the cosine is calculating (i.e. what's inside the brackets of the cosine)?
Last edited: