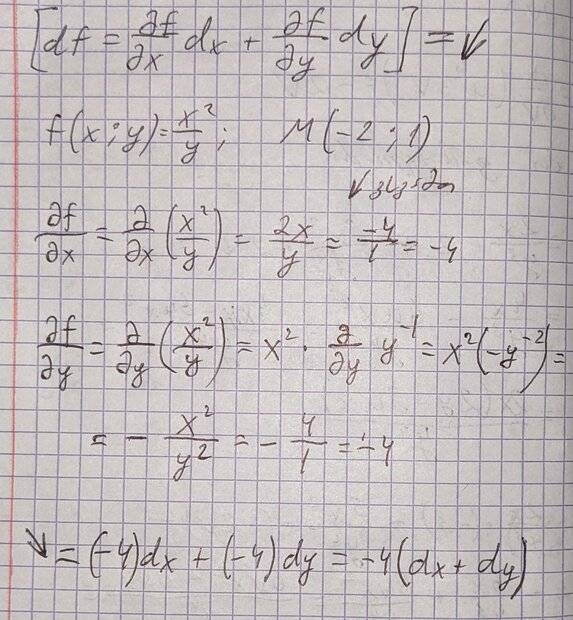SUMMARY
The discussion centers on the interpretation of a solution to a differential equation, specifically regarding the function f(x,y) = x^2/y evaluated at the point (-2,1). Participants clarify that the original poster has not presented a standard form of a differential equation, which typically appears as f' = g(x,y). The conversation emphasizes the importance of understanding the meaning behind the solution and its graphical representation.
PREREQUISITES
- Understanding of differential equations and their standard forms
- Familiarity with functions of multiple variables
- Basic knowledge of calculus, specifically derivatives
- Experience with graphical representation of mathematical functions
NEXT STEPS
- Research the standard forms of differential equations and their solutions
- Learn about evaluating functions at specific points
- Explore graphical tools for visualizing functions of two variables
- Study the concept of differentials and their applications in calculus
USEFUL FOR
Students studying calculus, mathematicians interested in differential equations, and educators looking to clarify the interpretation of mathematical solutions.